Question

20．已知0＜a＜1，在函数y=log_ax（x≥1）的图象上有A，B，C三点，它们的横坐标分别是t，t+2，t+4
（Ⅰ）若△ABC面积为S，求S=f（t）；
（Ⅱ）判断S=f（x）的单调性，求S=f（t）最大值．

Answer 1

分析 （Ⅰ）先画出对数函数的图象，根据S=$\frac{1}{2}$|A'C'|•|BD|求得三角形ABC的面积，再运用对数的运算性质对函数式化简；
（Ⅱ）根据复合函数单调性的判断法则确定f（t）的单调性，再求出函数的最大值．

解答 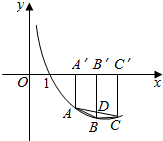（Ⅰ）如右所示，设A'、B'、C'是A、B、C在x轴上的射影，
则A（t，log_at），B（t+2，log_a（t+2）），C（t+4，log_a（t+4）），
设BB'与AC相交于点D，则可得D（t+2，$\frac{1}{2}$（log_at+log_a（t+4））），
于是S=f（t）=$\frac{1}{2}$|A'C'|•|BD|=$\frac{1}{2}$•4•[$\frac{1}{2}$（log_at+log_a（t+4））-log_a（t+2）]
=2log_a$\frac{\sqrt{t（t+4）}}{t+2}$=log_a$\frac{t^2+4t}{（t+2）^2}$（0＜a＜1，t≥1）；
（Ⅱ）∵x≥1，∴t≥1，∵S=f（t）=log_α$\frac{t^2+4t}{（t+2）^2}$=log_a[1-$\frac{4}{（t+4）^2}$]，
∴当t≥1时，u=（t+2）²是单调递增，$\frac{4}{（t+2）^2}$单调递增，
∵0＜α＜1，∴S=f（t）在[1，+∞）上是单调递减函数，
∵t≥1时，有$\frac{4}{（t+2）^2}$≤$\frac{4}{9}$，
∴1-$\frac{4}{（t+2）^2}$≥$\frac{5}{9}$，log_α[1-$\frac{4}{（t+4）^2}$]≤$lo{g}_{a}\frac{5}{9}$，
因此，S=f（t）的最大值是log_α$\frac{5}{9}$．

点评 本题主要考查了对数函数的图象与性质和复合函数单调性的判断，以及分类讨论，数形结合的解题思想，属于中档题．