
分析 (1)当a=3时,把不等式转化为与之等价的三个不等式组,求得每个不等式组的解集,再取并集,即得所求.
(2)由题意可得丨2x+l丨+丨2x-a丨+a>3的解集为R,由绝对值三角不等式可得丨2x+l丨+丨2x-a丨+a≥丨2x+l-2x+a丨+a=|a+1|+a,故有|a+1|+a>3,从而求得a的范围.
解答 解:(1)当a=3时,函数f(x)=丨2x+l丨+丨2x-3丨+3,
由f(x)>7,可得 $\left\{\begin{array}{l}{x<-\frac{1}{2}}\\{-2x-1-2x+3+3>7}\end{array}\right.$①,或 $\left\{\begin{array}{l}{-\frac{1}{2}≤x≤\frac{3}{2}}\\{2x+1-2x+3+3>7}\end{array}\right.$②,
或$\left\{\begin{array}{l}{x>\frac{3}{2}}\\{2x+1+2x-3+3>7}\end{array}\right.$③.
解①求得x<-$\frac{1}{2}$,解②求得x∈∅,解③求得x>$\frac{3}{2}$,
∴不等式f(x)>7的解集{x|x<-$\frac{1}{2}$或x>$\frac{3}{2}$}.
(2)若关于x的不等式f(x)>3的解集是R,
即丨2x+l丨+丨2x-a丨+a>3的解集为R.
而丨2x+l丨+丨2x-a丨+a≥丨2x+l-2x+a丨+a=|a+1|+a,
故有|a+1|+a>3,
∴$\left\{\begin{array}{l}{a+1≥0}\\{2a+1>3}\end{array}\right.$或$\left\{\begin{array}{l}{a+1<0}\\{-a-1+a>3}\end{array}\right.$
即a>1,
故a的范围为(1,+∞).
点评 本题主要考查绝对值不等式的解法,绝对值三角不等式,体现了等价转化、分类讨论的数学思想,属于中档题.


 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\frac{5}{3}$ | C. | $\frac{{\sqrt{37}}}{3}$ | D. | $\frac{{\sqrt{35}}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-2,-1] | B. | [1,2] | C. | [-2,1] | D. | [-1,2] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
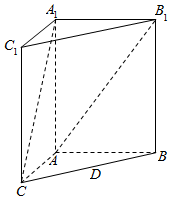 如图,在三棱柱ABC-A1B1C1中,四边形AA1C1C是边长为4的正方形,平面ABC⊥平面AA1C1C,AB=3,BC=5
如图,在三棱柱ABC-A1B1C1中,四边形AA1C1C是边长为4的正方形,平面ABC⊥平面AA1C1C,AB=3,BC=5查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com