
【题目】已知函数![]() ,
,![]() 为自然对数的底数.
为自然对数的底数.
(1)求证:当![]() 时,
时,![]() ;
;
(2)若函数![]() 有两个零点,求实数
有两个零点,求实数![]() 的取值范围.
的取值范围.
【答案】(1)见解析;(2)![]() .
.
【解析】
(1)构造![]() ,再求导可得
,再求导可得![]() ,再对导数求导,继而分析导函数的正负区间进而求得原函数的单调区间求最小值证明即可.
,再对导数求导,继而分析导函数的正负区间进而求得原函数的单调区间求最小值证明即可.
(2) 求导可得![]() ,再分
,再分![]() ,
,![]() ,
,![]() 分析函数的最小值,同时根据零点存在性定理判断是否有两个零点即可.
分析函数的最小值,同时根据零点存在性定理判断是否有两个零点即可.
(1)设![]() …
…
∴![]() ,
,
∴![]()
∵![]() ∴
∴![]() ∴
∴![]()
∴![]() 在
在![]() 上单调递增,
上单调递增,
又![]()
∴![]() 时,
时,![]()
∴![]() 在
在![]() 上单调递增,
上单调递增,
又![]()
∴![]() 时,
时,![]()
故当![]() 时,
时,![]() ;
;
(2)∵![]()
∴![]() ,
,
①当![]() 时,易知函数
时,易知函数![]() 只有一个零点,不符合题意;
只有一个零点,不符合题意;
②当![]() 时,在
时,在![]() 上,
上,![]() ,
,![]() 单调递减;在
单调递减;在![]() 上,
上,![]() ,
,![]() 单调递增;又
单调递增;又![]() ,且
,且![]() ,且当
,且当![]() 上,
上,![]() 恒成立,
恒成立,
又不妨取![]() 且
且![]() 时,
时,![]()
或者考虑:当![]()
所以函数![]() 在
在![]() 和在
和在![]() 上各有一个零点,即有两个零点.
上各有一个零点,即有两个零点.
③当![]() 时,由
时,由![]() 得
得![]() 或
或![]()
(i)当![]() 即
即![]() 时,在
时,在![]() 上,
上,![]() 成立,故
成立,故![]() 在
在![]() 上单调递增,所以函数
上单调递增,所以函数![]() 至多有一个零点,不符合题意
至多有一个零点,不符合题意
(ii)当![]() 即
即![]() 时,在
时,在![]() 和
和![]() 上,
上,![]() ,
,![]() 单调递增;
单调递增;
在![]() 上
上![]() ,
,![]() 单调递减;
单调递减;
又![]() ,且
,且![]() ,
,
所以函数![]() 至多有一个零点,不符合题意
至多有一个零点,不符合题意
(iii)当![]() 即
即![]() 时,在
时,在![]() 和
和![]() 上
上![]() ,
,![]() 单调递增;在
单调递增;在![]() 上
上![]() ,
,![]() 单调递减;又
单调递减;又![]() ,所以函数
,所以函数![]() 至多有一个零点,不符合题意
至多有一个零点,不符合题意
综上所述:实数![]() 的取值范围是
的取值范围是![]()


科目:高中数学 来源: 题型:
【题目】已知数列![]() 满足:
满足:![]() (常数
(常数![]() ),
),![]() ,(
,(![]() ,
,![]() ).数列
).数列![]() 满足:
满足:![]()
![]() .
.
(1)分别求![]() ,
,![]() ,
,![]() 的值:
的值:
(2)求数列![]() 的通项公式;
的通项公式;
(3)问:数列![]() 的每一项能否均为整数?若能,求出
的每一项能否均为整数?若能,求出![]() 的所有可能值;若不能,请说明理由.
的所有可能值;若不能,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】改革开放以来,我国农村7亿多贫困人口摆脱贫困,贫困发生率由1978年的97.5%下降到2018年底的1.4%,创造了人类减贫史上的中国奇迹,为全球减贫事业贡献了中国智慧和中国方案.“贫困发生率”是指低于贫困线的人口占全体人口的比例.2012年至2018年我国贫困发生率的数据如下表:
年份( | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 |
贫困发生率 | 10.2 | 8.5 | 7.2 | 5.7 | 4.5 | 3.1 | 1.4 |
(1)从表中所给的7个贫困发生率数据中任选两个,求至少有一个低于5%的概率;
(2)设年份代码![]() ,利用回归方程,分析2012年至2018年贫困发生率的变化情况,并预测2019年贫困发生率.
,利用回归方程,分析2012年至2018年贫困发生率的变化情况,并预测2019年贫困发生率.
附:回归直线![]() 的斜率和截距的最小二乘估计公式分别为:
的斜率和截距的最小二乘估计公式分别为: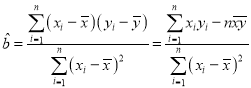 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在多面体![]() 中,四边形
中,四边形![]() 为矩形,
为矩形,![]() ,
,![]() 均为等边三角形,
均为等边三角形,![]() ,
,![]() .
.
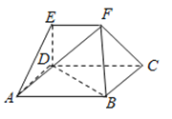
(Ⅰ)过![]() 作截面与线段
作截面与线段![]() 交于点
交于点![]() ,使得
,使得![]() 平面
平面![]() ,试确定点
,试确定点![]() 的位置,并予以证明;
的位置,并予以证明;
(Ⅱ)在(Ⅰ)的条件下,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的右焦点F到左顶点的距离为3.
的右焦点F到左顶点的距离为3.
(1)求椭圆C的方程;
(2)设O是坐标原点,过点F的直线与椭圆C交于A,B两点(A,B不在x轴上),若![]() ,延长AO交椭圆与点G,求四边形AGBE的面积S的最大值.
,延长AO交椭圆与点G,求四边形AGBE的面积S的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种产品的质量以其质量指标值衡量,质量指标值越大表明质量越好,记其质量指标值为M,当M≥85时,产品为一级品;当75≤M<85时,产品为二级品;当70≤M<75时,产品为三级品.现用两种新配方(分别称为A配方和B配方)做实验,各生产了100件这种产品,并测量了每件产品的质量指标值,得到下面试验结果:
A配方的频数分布表

B配方的频数分布表

(1)从A配方生产的产品中按等级分层抽样抽取5件产品,再从这5件产品中任取3件,求恰好取到1件二级品的频率;
(2)若这种新产品的利润率y与质量指标M满足如下条件: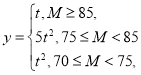 其中t∈
其中t∈![]() ,请分别计算两种配方生产的产品的平均利润率,如果从长期来看,你认为投资哪种配方的产品平均利润率较大?
,请分别计算两种配方生产的产品的平均利润率,如果从长期来看,你认为投资哪种配方的产品平均利润率较大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C的对边分别为a,b,c,满足acosB+bcosA=2ccosC.
(1)求角C的大小;
(2)若△ABC的周长为3,求△ABC的内切圆面积S的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在等腰梯形ABCD中,AB//CD,∠ABC=![]() ,BC=CD=CE=1,EC⊥平面ABCD,EF
,BC=CD=CE=1,EC⊥平面ABCD,EF![]() AC,P是线段EF上的动点
AC,P是线段EF上的动点
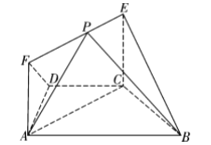
(1)求证:平面BCE⊥平面ACEF;
(2)求平面PAB与平面BCE所成锐二面角![]() 的最小值
的最小值
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com