
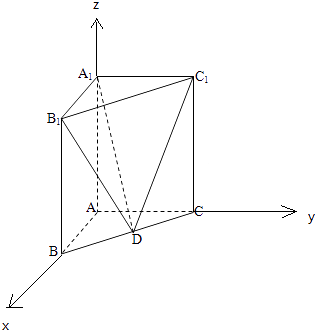
【题目】如图,在直三棱柱ABC﹣A1B1C1中,已知AB⊥AC,AB=2,AC=4,AA1=3.D是线段BC的中点. 
(1)求直线DB1与平面A1C1D所成角的正弦值;
(2)求二面角B1﹣A1D﹣C1的大小的余弦值.
【答案】
(1)解:因为在直三棱柱ABC﹣A1B1C1中,AB⊥AC,
所以分别以AB、AC、AA1所在的直线为x轴、y轴、z轴,建立空间直角坐标系,
则A(0,0,0),B(2,0,0),C(0,4,0),A1(0,0,3),B1(2,0,3),C1(0,4,3),
因为D是BC的中点,所以D(1,2,0),
因为 ![]() ,设平面A1C1D的法向量
,设平面A1C1D的法向量 ![]() ,
,
则 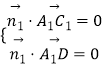 ,即
,即 ![]() ,取
,取 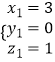 ,
,
所以平面A1C1D的法向量 ![]() ,而
,而 ![]() ,
,
所以 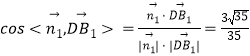 ,
,
所以直线DB1与平面A1C1D所成角的正弦值为 ![]()
(2)解: ![]() ,
, ![]() ,
,
设平面B1A1D的法向量 ![]() ,
,
则 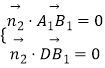 ,即
,即 ![]() ,
,
取  ,平面B1A1D的法向量
,平面B1A1D的法向量 ![]() ,
,
所以 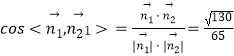 ,
,
二面角B1﹣A1D﹣C1的大小的余弦值 ![]() .
.
【解析】(1)分别以AB、AC、AA1所在的直线为x轴、y轴、z轴,建立空间直角坐标系,利用向量法能求出直线DB1与平面A1C1D所成角的正弦值.(2)求出平面B1A1D的法向量和平面B1A1D的法向量,利用向量法能求出二面角B1﹣A1D﹣C1的大小的余弦值.
【考点精析】根据题目的已知条件,利用空间角的异面直线所成的角的相关知识可以得到问题的答案,需要掌握已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则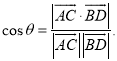 .
.


 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案科目:高中数学 来源: 题型:
【题目】 如图,在四棱锥P﹣ABCD中,侧面PAD⊥底面ABCD,侧棱PA=PD= ![]() ,PA⊥PD,底面ABCD为直角梯形,其中BC∥AD,AB⊥AD,AB=BC=1,O为AD中点.
,PA⊥PD,底面ABCD为直角梯形,其中BC∥AD,AB⊥AD,AB=BC=1,O为AD中点.

(1) 求直线PB与平面POC所成角的余弦值;
(2)线段![]() 上是否存在一点
上是否存在一点![]() ,使得二面角
,使得二面角![]() 的余弦值为
的余弦值为![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在数列{an}中,a1=2,an+1=4an-3n+1,n∈N*.
(1)求证:数列{an-n}是等比数列;
(2)求数列{an}的前n项和Sn;
(3)求证:不等式Sn+1≤4Sn对任意n∈N*皆成立.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学生对其亲属30人的饮食习惯进行了一次调查,并用下图所示的茎叶图表示30人的饮食指数.(说明:图中饮食指数低于70的人,饮食以蔬菜为主;饮食指数高于70的人,饮食以肉类为主)
(1)根据以上数据完成下面的2×2列联表:
主食 蔬菜 | 主食 肉类 | 总计 | |
50岁以下 | |||
50岁以上 | |||
总计 |
(2)能否在犯错误的概率不超过0.010的前提下认为“其亲属的饮食习惯与年龄有关”?并写出简要分析.
附参考公式:![]()
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an},其前n项和为Sn .
(1)若{an}是公差为d(d>0)的等差数列,且{ ![]() }也为公差为d的等差数列,求数列{an}的通项公式;
}也为公差为d的等差数列,求数列{an}的通项公式;
(2)若数列{an}对任意m,n∈N* , 且m≠n,都有 ![]() =am+an+
=am+an+ ![]() ,求证:数列{an}是等差数列.
,求证:数列{an}是等差数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系中,已知圆![]() 的圆心坐标为
的圆心坐标为![]() ,半径为
,半径为![]() ,以坐标原点为极点,
,以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系,直线l的参数方程为:
轴的正半轴为极轴建立极坐标系,直线l的参数方程为:![]() (
(![]() 为参数).
为参数).
(1)求圆![]() 和直线l的极坐标方程;
和直线l的极坐标方程;
(2)点![]() 的极坐标为
的极坐标为![]() ,直线l与圆
,直线l与圆![]() 相交于A,B,求
相交于A,B,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an},其前n项和为Sn .
(1)若{an}是公差为d(d>0)的等差数列,且{ ![]() }也为公差为d的等差数列,求数列{an}的通项公式;
}也为公差为d的等差数列,求数列{an}的通项公式;
(2)若数列{an}对任意m,n∈N* , 且m≠n,都有 ![]() =am+an+
=am+an+ ![]() ,求证:数列{an}是等差数列.
,求证:数列{an}是等差数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,A,B,C的对边分别是a,b,c,3sin2C+8sin2A=11sinAsinC,且c<2a.
(1)求证:△ABC为等腰三角形
(2)若△ABC的面积为8 ![]() .且sinB=
.且sinB= ![]() ,求BC边上的中线长.
,求BC边上的中线长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一块边长为![]() 的正三角形薄铁片,按如图所示设计方案,裁剪下三个全等的四边形(每个四边形中有且只有一组对角为直角),然后用余下的部分加工制作成一个“无盖”的正三棱柱(底面是正三角形的直棱柱)形容器.
的正三角形薄铁片,按如图所示设计方案,裁剪下三个全等的四边形(每个四边形中有且只有一组对角为直角),然后用余下的部分加工制作成一个“无盖”的正三棱柱(底面是正三角形的直棱柱)形容器.
(Ⅰ)请将加工制作出来的这个“无盖”的正三棱柱形容器的容积![]() 表示为关于
表示为关于![]() 的函数,并标明其定义域;
的函数,并标明其定义域;
(Ⅱ)若加工人员为了充分利用边角料,考虑在加工过程中,使用裁剪下的三个四边形材料恰好拼接成这个正三棱柱形容器的“顶盖”.
(1)请指出此时![]() 的值(不用说明理由),并求出这个封闭的正三棱柱形容器的侧面积
的值(不用说明理由),并求出这个封闭的正三棱柱形容器的侧面积![]() ;
;
(2)若还需要在该正三棱柱形容器中放入一个金属球体,试求该金属球体的最大体积![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com