【答案】
分析:对于①,先根据诱导公式进行化简,将

代入到函数f(x)中得到f(-

)的值为最小值,可判断直线

是

的一条对称轴,从而正确;对于②,将x=

代入到函数f(x)得到f(

)为函数f(x)的一个最大值,进而可知

不是

的对称中心,②不正确;对于③,根据f(

)=0,f(

)=-3可判断函数f(x)在区间

上不是增函数,可知③不正确;对于④根据左加右减的原则进行平移可知将y=-3sin2x的图象左平移

得到得图象不是函数
f(x),故④不正确.
解答:解:∵

=-3sin(2x-

)
将

代入到函数f(x)中得到f(-

)=-3sin(-

-

)=-3sin(-

)=-3
∴直线

是

的一条对称轴,故①正确;
将x=

代入到函数f(x)中得到f(

)=-3sin(

-

)=-3sin

=3

不是

的对称中心,故②不正确;
∵f(

)=3sin0=0,f(

)=3sin(-

+

)=-3,故函数f(x)在区间

上不是增函数
故③不正确;
将y=-3sin2x的图象左平移

得到y=-3sin2(x+

)=-3sin(2x+

)≠f(x)
故④不正确,
故答案为:①.
点评:本题主要考查正弦函数的基本性质--对称性、单调性的应用和三角函数的平移,三角函数的平移的原则是左加右减,上加下减.

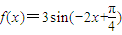 的图象为C,有下列四个命题:
的图象为C,有下列四个命题: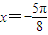 对称:
对称: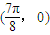 ;
;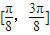 上是增函数;
上是增函数;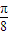 得到.其中真命题的序号是 .
得到.其中真命题的序号是 .  代入到函数f(x)中得到f(-
代入到函数f(x)中得到f(- )的值为最小值,可判断直线
)的值为最小值,可判断直线 是
是 的一条对称轴,从而正确;对于②,将x=
的一条对称轴,从而正确;对于②,将x= 代入到函数f(x)得到f(
代入到函数f(x)得到f( )为函数f(x)的一个最大值,进而可知
)为函数f(x)的一个最大值,进而可知 不是
不是 的对称中心,②不正确;对于③,根据f(
的对称中心,②不正确;对于③,根据f( )=0,f(
)=0,f( )=-3可判断函数f(x)在区间
)=-3可判断函数f(x)在区间 上不是增函数,可知③不正确;对于④根据左加右减的原则进行平移可知将y=-3sin2x的图象左平移
上不是增函数,可知③不正确;对于④根据左加右减的原则进行平移可知将y=-3sin2x的图象左平移 得到得图象不是函数
得到得图象不是函数 =-3sin(2x-
=-3sin(2x- )
) 代入到函数f(x)中得到f(-
代入到函数f(x)中得到f(- )=-3sin(-
)=-3sin(- -
- )=-3sin(-
)=-3sin(- )=-3
)=-3 是
是 的一条对称轴,故①正确;
的一条对称轴,故①正确; 代入到函数f(x)中得到f(
代入到函数f(x)中得到f( )=-3sin(
)=-3sin( -
- )=-3sin
)=-3sin =3
=3 不是
不是 的对称中心,故②不正确;
的对称中心,故②不正确; )=3sin0=0,f(
)=3sin0=0,f( )=3sin(-
)=3sin(- +
+ )=-3,故函数f(x)在区间
)=-3,故函数f(x)在区间 上不是增函数
上不是增函数 得到y=-3sin2(x+
得到y=-3sin2(x+ )=-3sin(2x+
)=-3sin(2x+ )≠f(x)
)≠f(x)

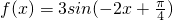 的图象为C,有下列四个命题:
的图象为C,有下列四个命题: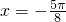 对称:
对称: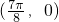 ;
;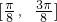 上是增函数;
上是增函数; 得到.其中真命题的序号是 ________.
得到.其中真命题的序号是 ________.