
【题目】已知x∈R,[x]表示不超过x的最大整数,若函数 ![]() 有且仅有3个零点,则实数a的取值范围是.
有且仅有3个零点,则实数a的取值范围是.
【答案】![]()
【解析】解:由 ![]() 得
得 ![]() =2a, ①若x>0,设g(x)=
=2a, ①若x>0,设g(x)= ![]() ,
,
则当0<x<1,[x]=0,此时g(x)=0,
当1≤x<2,[x]=1,此时g(x)= ![]() ,此时
,此时 ![]() <g(x)≤1,
<g(x)≤1,
当2≤x<3,[x]=2,此时g(x)= ![]() ,此时
,此时 ![]() <g(x)≤1,
<g(x)≤1,
当3≤x<4,[x]=3,此时g(x)= ![]() ,此时
,此时 ![]() <g(x)≤1,
<g(x)≤1,
当4≤x<5,[x]=4,此时g(x)= ![]() ,此时
,此时 ![]() <g(x)≤1,
<g(x)≤1,
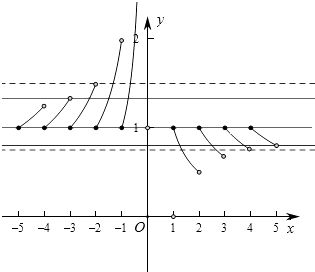
作出函数g(x)的图象,
要使 ![]() 有且仅有三个零点,
有且仅有三个零点,
即函数g(x)=2a有且仅有三个零点,
则由图象可知 ![]() <a≤
<a≤ ![]() ,
,
②若x<0,设g(x)= ![]() ,
,
则当﹣1≤x<0,[x]=﹣1,此时g(x)=﹣ ![]() ,此时g(x)≥1,
,此时g(x)≥1,
当﹣2≤x<﹣1,[x]=﹣2,此时g(x)=﹣ ![]() ,此时1≤g(x)<2,
,此时1≤g(x)<2,
当﹣3≤x<﹣2,[x]=﹣3,此时g(x)=﹣ ![]() ,此时1≤g(x)<
,此时1≤g(x)< ![]() ,
,
当﹣4≤x<﹣3,[x]=﹣4,此时g(x)=﹣ ![]() ,此时1≤g(x)<
,此时1≤g(x)< ![]() ,
,
当﹣5≤x<﹣4,[x]=﹣5,此时g(x)=﹣ ![]() ,此时1≤g(x)<
,此时1≤g(x)< ![]() ,
,
作出函数g(x)的图象,
要使 ![]() 有且仅有三个零点,
有且仅有三个零点,
即函数g(x)=2a有且仅有三个零点,
则由图象可知 ![]() ≤a<
≤a< ![]() ,
,
综上: ![]() <a≤
<a≤ ![]() 或
或 ![]() ≤a<
≤a< ![]() ,
,
所以答案是: ![]() .
.
【考点精析】解答此题的关键在于理解函数的零点与方程根的关系的相关知识,掌握二次函数的零点:(1)△>0,方程 有两不等实根,二次函数的图象与 轴有两个交点,二次函数有两个零点;(2)△=0,方程 有两相等实根(二重根),二次函数的图象与 轴有一个交点,二次函数有一个二重零点或二阶零点;(3)△<0,方程 无实根,二次函数的图象与 轴无交点,二次函数无零点.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2﹣2ax+a.
(1)若对任意的实数x都有f(1+x)=f(1﹣x)成立,求实数a的值;
(2)若f(x)在区间[1,+∞)上为单调增函数,求实数a的取值范围;
(3)当x∈[﹣1,1]时,求函数f(x)的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】等比数列{an}的各项均为正数,且2a1+3a2=1, ![]() =9a2a6.
=9a2a6.
(1)求数列{an}的通项公式;
(2)设bn=log3a1+log3a2+…+log3an,求数列![]() 的前n项和.
的前n项和.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若不等式|2x﹣1|﹣|x+a|≥a对任意的实数x恒成立,则实数a的取值范围是( )
A.(﹣∞,﹣ ![]() ]
]
B.(﹣ ![]() ,﹣
,﹣ ![]() ]
]
C.(﹣ ![]() ,0)
,0)
D.(﹣∞,﹣ ![]() ]
]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】要得到函数y=sin2x的图象,只要将y=sin(2x+ ![]() )函数的图象( )
)函数的图象( )
A.向左平移 ![]() 个单位
个单位
B.向右平移 ![]() 个单位
个单位
C.向左平移 ![]() 个单位
个单位
D.向右平移 ![]() 个单位
个单位
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com