
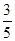 ,甲胜丙的概率为
,甲胜丙的概率为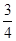 ,乙胜丙的概率为
,乙胜丙的概率为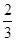 。比赛顺序为:首先由甲和乙进行第一局的比赛,再由获胜者与未参加比赛的选手进行第二局的比赛,依此类推,在比赛中,有选手获胜满两局就取得比赛的胜利,比赛结束。
。比赛顺序为:首先由甲和乙进行第一局的比赛,再由获胜者与未参加比赛的选手进行第二局的比赛,依此类推,在比赛中,有选手获胜满两局就取得比赛的胜利,比赛结束。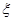 ,求
,求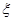 的概率分布列和数学期望
的概率分布列和数学期望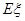 。
。 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:不详 题型:解答题
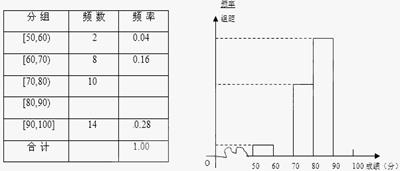
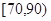 段的有多少人;
段的有多少人;查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
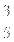 。
。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| | 关注NBA | 不关注NBA | 合 计 |
| 男 生 | | 6 | |
| 女 生 | 10 | | |
| 合 计 | | | 48 |
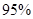 的把握认为关注NBA与性别有关?
的把握认为关注NBA与性别有关?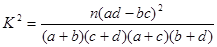 ,其中
,其中 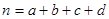
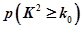 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
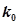 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
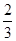 ,没有平局.采用三局两胜制比赛,即先胜两局者获胜且比赛结束,则甲队获胜的概率等于( )
,没有平局.采用三局两胜制比赛,即先胜两局者获胜且比赛结束,则甲队获胜的概率等于( )A.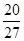 | B.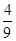 | C.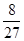 | D.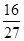 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
A.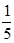 | B.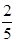 | C.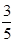 | D.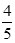 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com