
【题目】已知函数![]() .
.
(1)若![]() ,
,![]() ,求
,求![]() 的值域;
的值域;
(2)当![]() 时,求
时,求![]() 的最小值
的最小值![]() ;
;
(3)是否存在实数![]() 、
、![]() ,同时满足下列条件:①
,同时满足下列条件:① ![]() ;② 当
;② 当![]() 的定义域为
的定义域为![]() 时,其值域为
时,其值域为![]() .若存在,求出
.若存在,求出![]() 、
、![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【答案】(1) ![]() (2)
(2) 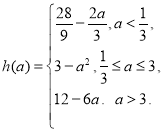 (3) 不存在满足条件的实数
(3) 不存在满足条件的实数![]() 、
、![]() .见解析
.见解析
【解析】
(1)设t=3x,则φ(t)=t2﹣2at+3=(t﹣a)2+3﹣a2,φ(t)的对称轴为t=a,当a=1时,即可求出f(x)的值域;
(2)由函数φ(t)的对称轴为t=a,分类讨论当a![]() 时,当
时,当![]() a≤3时,当a>3时,求出最小值,则h(a)的表达式可求;
a≤3时,当a>3时,求出最小值,则h(a)的表达式可求;
(3)假设满足题意的m,n存在,函数h(a)在(3,+∞)上是减函数,求出h(a)的定义域,值域,然后列出不等式组,求解与已知矛盾,即可得到结论.
(1)当![]() 时,由
时,由![]() ,得
,得![]() ,
,
因为![]() ,所以
,所以![]() ,
,![]() .
.
(2)令![]() ,因为
,因为![]() ,故
,故![]() ,函数
,函数![]() 可化为
可化为
![]() .
.
① 当![]() 时,
时,![]() ;
;
② 当![]() 时,
时,![]() ;
;
③ 当![]() 时,
时,![]() .
.
综上,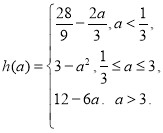
(3)因为![]() ,
,![]() 为减函数,
为减函数,
所以![]() 在
在![]() 上的值域为
上的值域为![]() ,
,
又![]() 在
在![]() 上的值域为
上的值域为![]() ,所以,
,所以,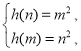 即
即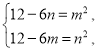
两式相减,得![]() ,
,
因为![]() ,所以
,所以![]() ,而由
,而由![]() 可得
可得![]() ,矛盾.
,矛盾.
所以,不存在满足条件的实数![]() 、
、![]() .
.


科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() 为自然对数的底数).
为自然对数的底数).
(1)求函数![]() 的极值;
的极值;
(2)问:是否存在实数![]() ,使得
,使得![]() 有两个相异零点?若存在,求出
有两个相异零点?若存在,求出![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的长轴是短轴的两倍,以短轴一个顶点和长轴一个顶点为端点的线段作直径的圆的周长等于
的长轴是短轴的两倍,以短轴一个顶点和长轴一个顶点为端点的线段作直径的圆的周长等于![]() ,直线l与椭圆C交于
,直线l与椭圆C交于![]() 两点.
两点.
(1)求椭圆C的方程;
(2)过点O作直线l的垂线,垂足为D.若![]() ,求动点D的轨迹方程.
,求动点D的轨迹方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是2017年第一季度五省GDP情况图,则下列陈述中不正确的是( )
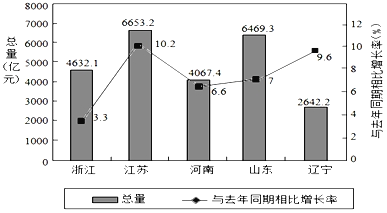
A.2017年第一季度GDP增速由高到低排位第5的是浙江省.
B.与去年同期相比,2017年第一季度的GDP总量实现了增长.
C.2017年第一季度GDP总量和增速由高到低排位均居同一位的省只有1个
D.去年同期河南省的GDP总量不超过4000亿元.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() ,
,![]() 满足
满足![]() (
(![]() …).
…).
(1)若![]() ,求
,求![]() 的值;
的值;
(2)若![]() 且
且![]() ,则数列
,则数列![]() 中第几项最小?请说明理由;
中第几项最小?请说明理由;
(3)若![]() (n=1,2,3,…),求证:“数列
(n=1,2,3,…),求证:“数列![]() 为等差数列”的充分必要条件是“数列
为等差数列”的充分必要条件是“数列![]() 为等差数列且
为等差数列且![]() (n=1,2,3,…)”.
(n=1,2,3,…)”.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于定义域为![]() 的函数
的函数![]() ,如果存在区间
,如果存在区间![]() ,其中
,其中![]() ,同时满足:
,同时满足:
①![]() 在
在![]() 内是单调函数:②当定义域为
内是单调函数:②当定义域为![]() 时,
时,![]() 的值域为
的值域为![]() ,则称函数
,则称函数![]() 是区间
是区间![]() 上的“保值函数”,区间
上的“保值函数”,区间![]() 称为“保值函数”.
称为“保值函数”.
(1)求证:函数![]() 不是定义域
不是定义域![]() 上的“保值函数”;
上的“保值函数”;
(2)若函数![]() (
(![]() )是区间
)是区间![]() 上的“保值函数”,求
上的“保值函数”,求![]() 的取值范围;
的取值范围;
(3)对(2)中函数![]() ,若不等式
,若不等式![]() 对
对![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2018届安徽省合肥市高三第一次教学质量检测】一家大型购物商场委托某机构调查该商场的顾客使用移动支付的情况.调查人员从年龄在![]() 内的顾客中,随机抽取了180人,调查结果如表:
内的顾客中,随机抽取了180人,调查结果如表:

(1)为推广移动支付,商场准备对使用移动支付的顾客赠送1个环保购物袋.若某日该商场预计有12000人购物,试根据上述数据估计,该商场当天应准备多少个环保购物袋?
(2)某机构从被调查的使用移动支付的顾客中,按分层抽样的方式抽取7人作跟踪调查,并给其中2人赠送额外礼品,求获得额外礼品的2人年龄都在![]() 内的概率.
内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的离心率
的离心率![]() ,且圆
,且圆![]() 过椭圆
过椭圆![]() 的上,下顶点.
的上,下顶点.
(1)求椭圆![]() 的方程.
的方程.
(2)若直线![]() 的斜率为
的斜率为![]() ,且直线
,且直线![]() 交椭圆
交椭圆![]() 于
于![]() 、
、![]() 两点,点
两点,点![]() 关于点的对称点为
关于点的对称点为![]() ,点
,点![]() 是椭圆
是椭圆![]() 上一点,判断直线
上一点,判断直线![]() 与
与![]() 的斜率之和是否为定值,如果是,请求出此定值:如果不是,请说明理.
的斜率之和是否为定值,如果是,请求出此定值:如果不是,请说明理.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com