
已知向量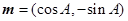 ,
,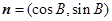 ,
,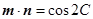 ,其中
,其中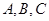 为
为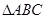 的内角.
的内角.
(Ⅰ)求角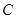 的大小;
的大小;
(Ⅱ)若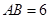 ,且
,且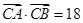 ,求
,求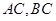 的长.
的长.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
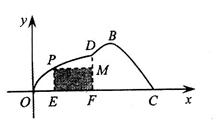
如图,某市准备在一个湖泊的一侧修建一条直路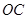 ,另一侧修建一条观光大道,它的前一段
,另一侧修建一条观光大道,它的前一段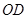 是以
是以 为顶点,
为顶点,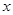 轴为对称轴,开口向右的抛物线的一部分,后一段
轴为对称轴,开口向右的抛物线的一部分,后一段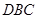 是函数
是函数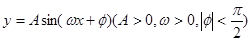 ,
,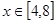 时的图象,图象的最高点为
时的图象,图象的最高点为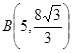 ,
,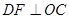 ,垂足为
,垂足为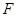 .
.
(1)求函数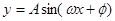 的解析式;
的解析式;
(2)若在湖泊内修建如图所示的矩形水上乐园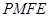 ,问:点
,问:点 落在曲线
落在曲线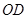 上何处时,水上乐园的面积最大?
上何处时,水上乐园的面积最大?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某同学在一次研究性学习中发现,以下五个式子的值都等于同一个常数 .
.
①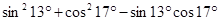 ;
;
②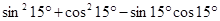 ;
;
③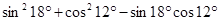 ;
;
④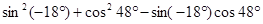 ;
;
⑤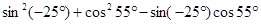 .
.
(1)从上述五个式子中选择一个,求出常数 ;
;
(2)根据(1)的计算结果,将该同学的发现推广为一个三角恒等式,并证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某单位有 、
、 、
、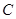 三个工作点,需要建立一个公共无线网络发射点
三个工作点,需要建立一个公共无线网络发射点 ,使得发射点到三个工作点的距离相等.已知这三个工作点之间的距离分别为
,使得发射点到三个工作点的距离相等.已知这三个工作点之间的距离分别为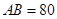
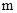 ,
,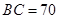
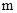 ,
,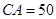
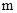 .假定
.假定 、
、 、
、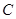 、
、 四点在同一平面上.
四点在同一平面上.
(1)求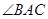 的大小;
的大小;
(2)求点 到直线
到直线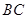 的距离.
的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数f(x)=2sin(ωx),其中常数ω>0
(1)令ω=1,判断函数F(x)=f(x)+f(x+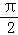 )的奇偶性,并说明理由;
)的奇偶性,并说明理由;
(2)令ω=2,将函数y=f(x)的图象向左平移个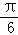 单位,再向上平移1个单位,得到函数y=g(x)的图象,对任意a∈R,求y=g(x)在区间[a,a+10π]上零点个数的所有可能值.
单位,再向上平移1个单位,得到函数y=g(x)的图象,对任意a∈R,求y=g(x)在区间[a,a+10π]上零点个数的所有可能值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com