
【题目】已知函数f(x)=lnx﹣sinx,记f(x)的导函数为f'(x).
(1)若h(x)=ax![]() f'(x)是(0,+∞)上的单调递增函数,求实数a的取值范围;
f'(x)是(0,+∞)上的单调递增函数,求实数a的取值范围;
(2)若x∈(0,2π),试判断函数f(x)的极值点个数,并说明理由.
【答案】(1)a≥1;(2)函数f(x)在(0,2π)上有且仅有唯一的极大值点,无极小值点;理由详见解析
【解析】
(1)只需h′(x)≥0在(0,+∞)恒成立,借助于三角函数的有界性,问题可解决.
(2)分x∈(0,1),![]() ,
,![]() ,
,![]() 四种情形分别研究f(x)的单调性,进而得出结论.
四种情形分别研究f(x)的单调性,进而得出结论.
解:(1)∵![]() ,
,
∴![]() ax+cosx,因为h(x)是(0,+∞)上的单调递增函数,
ax+cosx,因为h(x)是(0,+∞)上的单调递增函数,
∴h′(x)=a﹣sinx≥0(x>0)恒成立,因为sinx∈[﹣1,1],
故a≥1时,h′(x)≥0恒成立,且导数为0时不连续.
故a≥1即为所求.
(2)由(1)知,![]() ,
,
①当x∈(0,1]时,f′(x)≥1﹣cosx>0,
此时函数f(x)单调递增,无极值点;
②当![]() 时,则
时,则![]() ,
,
∵![]() ,而由三角函数的性质可知,
,而由三角函数的性质可知,![]() ,
,
∴![]() ,
,
此时函数f(x)单调递增,无极值点;
③当![]() 时,cosx<0,则
时,cosx<0,则![]() ,
,
此时函数f(x)单调递增,无极值点;
④当![]() 时,令
时,令![]() ,则
,则![]() ,
,
∴函数g(x)单调递减,
又![]() ,
,
∴存在唯一的![]() ,使得g(x0)=0,
,使得g(x0)=0,
且当![]() 时,g(x)=f′(x)>0,f(x)单调递增,
时,g(x)=f′(x)>0,f(x)单调递增,
当x∈(x0,2π)时,g(x)=f′(x)<0,f(x)单调递减,
故x0是函数f(x)的极大值点,
综上所述,函数f(x)在(0,2π)上有且仅有唯一的极大值点,无极小值点.


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:高中数学 来源: 题型:
【题目】如图,在正方体![]() 中,P,Q,M,N,H,R是各条棱的中点.
中,P,Q,M,N,H,R是各条棱的中点.
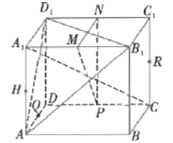
①直线![]() 平面
平面![]() ;②
;②![]() ;③P,Q,H,R四点共面;④
;③P,Q,H,R四点共面;④![]() 平面
平面![]() .其中正确的个数为( )
.其中正确的个数为( )
A.1B.2C.3D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年底,武汉发生“新型冠状病毒”肺炎疫情,国家卫健委紧急部署,从多省调派医务工作者前去支援,正值农历春节举家团圆之际,他们成为“最美逆行者”.武汉市从2月7日起举全市之力入户上门排查确诊的新冠肺炎患者疑似的新冠肺炎患者无法明确排除新冠肺炎的发热患者和确诊患者的密切接触者等“四类”人员,强化网格化管理,不落一户不漏一人.若在排查期间,某小区有5人被确认为“确诊患者的密切接触者”,现医护人员要对这5人随机进行逐一“核糖核酸”检测,只要出现一例阳性,则将该小区确定为“感染高危小区”.假设每人被确诊的概率均为![]() 且相互独立,若当
且相互独立,若当![]() 时,至少检测了4人该小区被确定为“感染高危小区”的概率取得最大值,则
时,至少检测了4人该小区被确定为“感染高危小区”的概率取得最大值,则![]() ____.
____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正四棱锥![]() 的侧棱和底面边长相等,在这个正四棱锥的
的侧棱和底面边长相等,在这个正四棱锥的![]() 条棱中任取两条,按下列方式定义随机变量
条棱中任取两条,按下列方式定义随机变量![]() 的值:
的值:
若这两条棱所在的直线相交,则![]() 的值是这两条棱所在直线的夹角大小(弧度制);
的值是这两条棱所在直线的夹角大小(弧度制);
若这两条棱所在的直线平行,则![]() ;
;
若这两条棱所在的直线异面,则![]() 的值是这两条棱所在直线所成角的大小(弧度制).
的值是这两条棱所在直线所成角的大小(弧度制).
(1)求![]() 的值;
的值;
(2)求随机变量![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() 的离心率
的离心率![]() ,左焦点为
,左焦点为![]() ,右顶点为
,右顶点为![]() ,过点
,过点![]() 的直线交椭圆于
的直线交椭圆于![]() 两点,若直线
两点,若直线![]() 垂直于
垂直于![]() 轴时,有
轴时,有![]() .
.
(1)求椭圆的方程;
(2)设直线![]() :
: ![]() 上两点
上两点![]() ,
, ![]() 关于
关于![]() 轴对称,直线
轴对称,直线![]() 与椭圆相交于点
与椭圆相交于点![]() (
(![]() 异于点
异于点![]() ),直线
),直线![]() 与
与![]() 轴相交于点
轴相交于点![]() .若
.若![]() 的面积为
的面积为![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市场研究人员为了了解产业园引进的甲公司前期的经营状况,对该公司2019年连续六个月的利润进行了统计,并根据得到的数据绘制了相应的折线图,如图所示:
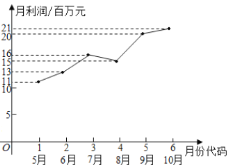
(1)由折线图可以看出,可用线性回归模型拟合月利润![]() (单位:百万元)与月份代码
(单位:百万元)与月份代码![]() 之间的关系,求
之间的关系,求![]() 关于
关于![]() 的线性回归方程,并预测该公司2020年4月份的利润;
的线性回归方程,并预测该公司2020年4月份的利润;
(2)甲公司新研制了一款产品,需要采购一批新型材料,现有A,B两种型号的新型材料可供选择,按规定每种新型材料最多可使用4个月,但新材料的不稳定性会导致材料的使用寿命不同,现对A,B两种型号的新型材料对应的产品各100件进行科学模拟测试,得到两种新型材料使用寿命的频数统计如下表:

经甲公司测算平均每件新型材料每月可以带来6万元收人入,不考虑除采购成本之外的其他成本,A型号材料每件的采购成本为10万元,B型号材料每件的采购成本为12万元.假设每件新型材料的使用寿命都是整月数,且以频率作为每件新型材料使用寿命的概率,如果你是甲公司的负责人,以每件新型材料产生利润的平均值为决策依据,你会选择采购哪款新型材料?
参考数据:![]() ,
,![]() .
.
参考公式:回归直线方程![]() ,其中
,其中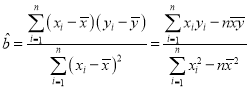 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为弘扬新时代的中国女排精神.甲、乙两个女排校队举行一场友谊比赛,采用五局三胜制(即某队先赢三局则获胜,比赛随即结束).若两队的竞技水平和比赛状态相当,且每局比赛相互独立,则比赛结束时已经进行的比赛局数的数学期望是______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】厂家在产品出厂前,需对产品做检验,第一次检测厂家的每件产品合格的概率为![]() ,如果合格,则可以出厂;如果不合格,则进行技术处理,处理后进行第二次检测.每件产品的合格率为
,如果合格,则可以出厂;如果不合格,则进行技术处理,处理后进行第二次检测.每件产品的合格率为![]() ,如果合格,则可以出厂,不合格则当废品回收.
,如果合格,则可以出厂,不合格则当废品回收.
![]() 求某件产品能出厂的概率;
求某件产品能出厂的概率;
![]() 若该产品的生产成本为
若该产品的生产成本为![]() 元/件,出厂价格为
元/件,出厂价格为![]() 元/件,每次检测费为
元/件,每次检测费为![]() 元/件,技术处理每次
元/件,技术处理每次![]() 元/件,回收获利
元/件,回收获利![]() 元/件.假如每件产品是否合格相互独立,记
元/件.假如每件产品是否合格相互独立,记![]() 为任意一件产品所获得的利润,求随机变量
为任意一件产品所获得的利润,求随机变量![]() 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com