练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

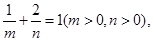    已知当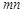取得最小值时，直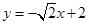线与曲线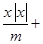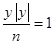的交点个数为             

    2

    解析试题分析：∵，
    ∴当且仅当，即时，取得最小值8，
    故曲线方程为时，方程化为；
    当时，方程化为，
    当时，方程化为，
    当时，无意义，
    由圆锥曲线可作出方程和直线与的图象，
    由图象可知，交点的个数为2.

    考点：基本不等式，直线与圆锥曲线的位置关系.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    （07年朝阳区一模）（14分）  已知双曲线的中心在原点O，右焦点为F（c，0），P是双曲线右支上一点，且△OEP的面积为

       （Ⅰ）若点P的坐标为，求此双曲线的离心率；

       （Ⅱ）若，当取得最小值时，求此双曲线的方程.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知△OFQ的面积为26，且·=m.

    （1）设＜m＜4，求向量与的夹角θ正切值的取值范围；

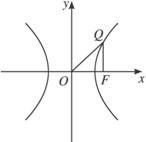
    （2）设以O为中心，F为焦点的双曲线经过点Q（如图），||=c，m(-1)c2,当?||取得最小值时，求此双曲线的方程.

    查看答案和解析>>

    科目：高中数学 来源：2014届山西省高三9月月考理科数学试卷（解析版） 题型：填空题

    已知当取得最小值时，直线与曲线的交点个数为             

     

    查看答案和解析>>

    科目：高中数学 来源：2011年广东省高三下学期期初考试数学文卷 题型：解答题

    （本小题满分12分）

    已知，且．

       （1）若为的三内角，当取得最小值时，求；

       （2）当时，将函数的图象按向量平移后得到函数的图象，求出所有满足条件的向量．

     

    查看答案和解析>>

    同步练习册答案