
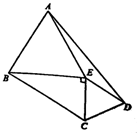
分析 (Ⅰ)求出BE,AE=BE=$\sqrt{3}$,DE=CE=1,∠AED=150°,利用余弦定理求线段AD的长;
(Ⅱ)比较∠ADC和∠ABC的大小,转化为比较∠ADE与∠EBC的大小.
解答 解:(Ⅰ)在Rt△BEC中,CE=1,∠EBC=30°,∴BE=$\sqrt{3}$,
在△ADE中,AE=BE=$\sqrt{3}$,DE=CE=1,∠AED=150°,
由余弦定理可得AD=$\sqrt{3+1-2×\sqrt{3}×1×(-\frac{\sqrt{3}}{2})}$=$\sqrt{7}$;
(Ⅱ)∵∠ADC=∠ADE+60°,∠ABC=∠EBC+60°,
∴问题转化为比较∠ADE与∠EBC的大小.
在△ADE中,由正弦定理可得$\frac{sin∠ADE}{AE}=\frac{sin∠AED}{AD}$,
∴sin∠ADE=$\frac{\frac{1}{2}×\sqrt{3}}{\sqrt{7}}$<$\frac{1}{2}$=sin30°,
∴∠ADE<30°
∴∠ADC<∠ABC.
点评 本题考查余弦定理的运用,考查正弦定理,考查学生分析解决问题的能力,正确运用正弦、余弦定理是关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | ($\frac{2}{7},-3$) | B. | (-2,-3) | C. | (0,$\frac{2}{7}$) | D. | (-2,0) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 即不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a?α,b⊥β,α∥β | B. | a⊥α,b⊥β,α∥β | C. | a∥α,b∥β,α⊥β | D. | a?α,b∥β,α⊥β |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
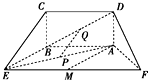 如图所示的五面体中,四边形ABCD是矩形,AD⊥平面ABEF,AB∥EF,且AD=1,AB=$\frac{1}{2}$EF=2$\sqrt{2}$,AF=BE=2,点P、Q、M分别为AE、BD、EF的中点.
如图所示的五面体中,四边形ABCD是矩形,AD⊥平面ABEF,AB∥EF,且AD=1,AB=$\frac{1}{2}$EF=2$\sqrt{2}$,AF=BE=2,点P、Q、M分别为AE、BD、EF的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com