
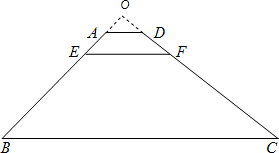
 解:延长BA与CD交于点O,如下图所示:
解:延长BA与CD交于点O,如下图所示:

 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
 (2012•江西)如图,在梯形ABCD中,AB∥CD,E,F是线段AB上的两点,且DE⊥AB,CF⊥AB,AB=12,AD=5,BC=4
(2012•江西)如图,在梯形ABCD中,AB∥CD,E,F是线段AB上的两点,且DE⊥AB,CF⊥AB,AB=12,AD=5,BC=4| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:

查看答案和解析>>
科目:高中数学 来源: 题型:
[2012·江西卷] 如图1-7,在梯形ABCD中,AB∥CD,E,F是线段AB上的两点,且DE⊥AB,CF⊥AB,AB=12,AD=5,BC=4![]() ,DE=4,现将△ADE,△CFB分别沿DE,CF折起,使A,B两点重合于点G,得到多面体CDEFG.
,DE=4,现将△ADE,△CFB分别沿DE,CF折起,使A,B两点重合于点G,得到多面体CDEFG.
(1)求证:平面DEG⊥平面CFG;
(2)求多面体CDEFG的体积.
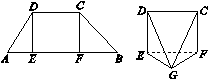
图1-7
查看答案和解析>>
科目:高中数学 来源:2012-2013学年广东省江门市新会一中高三(上)第四次检测数学试卷(理科)(解析版) 题型:解答题
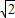 ,DE=4.现将△ADE,△CFB分别沿DE,CF折起,使A,B两点重合与点G,得到多面体CDEFG.
,DE=4.现将△ADE,△CFB分别沿DE,CF折起,使A,B两点重合与点G,得到多面体CDEFG.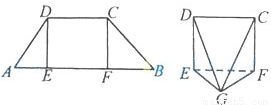
查看答案和解析>>
科目:高中数学 来源:2012年江西省高考数学试卷(文科)(解析版) 题型:解答题
 ,DE=4.现将△ADE,△CFB分别沿DE,CF折起,使A,B两点重合与点G,得到多面体CDEFG.
,DE=4.现将△ADE,△CFB分别沿DE,CF折起,使A,B两点重合与点G,得到多面体CDEFG.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com