Question

在等差数列{a_n}中,公差d＞0,其前n项和是S_n,a₂a₃=45,a₁+a₄=14.

(1)求数列{a_n}的通项公式；

(2)设b_n=(其中c是非零常数),若数列{b_n}是等差数列,求c的值.

Answer 1

思路解析:对于第一个问题,不难由已知条件转而确定a₁与d的值,最基本的方法就是根据通项公式列出相应方程组,从而求解；对于第二个问题,要求使数列{b_n}是等差数列的c值,可以根据定义去确定,但那样做计算量较大,于是可以先找到相应的必要条件,即先考虑使其前三项成等差数列的c值,再检验即可.

解:(1)由已知得a₂+a₃=a₁+a₄=14.

又a₂a₃=45,

故a₂、a₃是方程x²-14x+45=0的两根,而其两根分别为5,9,

又公差?d＞0,故有a₂＜a₃,a₂=5,a₃=9,d=a₃-a₂=4,a₁=a₂-d=1,a_n=4n-3.

(2)由(1)以及已知得S_n==2n²-n,b_n=,b₁=,b₂=,

b₃=,又数列{b_n}是等差数列,故有2b₂=b₁+b₃,即2×,

由此解得 (其中c=0舍去),且当时,b_n=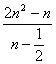=2n,数列{b_n}是等差数列,故为所求.