
 如图,Rt△AB′C′是由Rt△ABC绕点A顺时针旋转得到的,连结CC′交斜边于点E,CC′的延长线交BB′于点F.
如图,Rt△AB′C′是由Rt△ABC绕点A顺时针旋转得到的,连结CC′交斜边于点E,CC′的延长线交BB′于点F.分析 (1)欲证△ACE∽△FBE,通过观察发现两个三角形已经具备一组角对应相等,即∠AEC=∠FEB,此时,再证∠AC′C=∠ABB′即可.
(2)欲证△ACE≌△FBE,由(1)知△ACE∽△FBE,只需证明CE=BE,由已知可证∠ABC=∠BCE=α,即证β=2α时,△ACE≌△FBE.
解答 (1)证明:∵Rt△AB′C′是由Rt△ABC绕点A顺时针旋转得到的,
∴AC=AC′,AB=AB′,∠CAB=∠C′AB′,
∴∠CAC′=∠BAB′
∴∠ACC′=∠ABB′
又∠AEC=∠FEB,
∴△ACE∽△FBE
(2)解:当β=2α时,△ACE≌△FBE.
在△ACC′中,∵AC=AC′,∴$∠ACC'=\frac{180°-∠CAC'}{2}=\frac{180°-β}{2}=90°-α$
在Rt△ABC中,∠ACC′+∠BCE=90°,即90°-α+∠BCE=90°,
∴∠BCE=α∵∠ABC=α,∴∠ABC=∠BCE,∴CE=BE
由(1)知:△ACE∽△FBE,∴△ACE≌△FBE.
点评 本题考查相似三角形的判定.识别两三角形相似,除了要掌握定义外,还要注意正确找出两三角形的对应边、对应角,可利用数形结合思想根据图形提供的数据计算对应角的度数、对应边的比.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | 2 | B. | $\sqrt{2}$ | C. | 2$\sqrt{2}$ | D. | 4$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
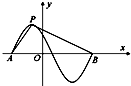 函数f(x)=cos(πx+φ)(φ>0)的图象如图所示,设P是图象的最高点,A、B是图象与x轴的交点,则tan∠APB=( )
函数f(x)=cos(πx+φ)(φ>0)的图象如图所示,设P是图象的最高点,A、B是图象与x轴的交点,则tan∠APB=( )| A. | 10 | B. | 8 | C. | $\frac{8}{7}$ | D. | $\frac{4}{7}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com