
 给出下列结论:
给出下列结论:分析 根据系统抽样,可判断①;给出不等式的解集,可判断②;根据概率的稳定性,可判断③;求出棱锥的侧面积,可判断④.
解答 解:①从编号为1~50的50枚导弹中,采用系统抽样方法抽取5枚来进行发射实验,则组距为10,
故所选取5枚导弹的编号可能是3,13,23,33,43,故①正确;
②若f(x)为R上的偶函数,且在(-∞,0]内是减函数,f(-2)=0,
∴f(x)在[0,+∞)内是增函数,f(2)=0,
则f(x)>0的解集为(-∞,-2)∪(2,+∞),故②错误.
③掷一枚硬币,连续出现5次正面向上,第六次出现反面向上的概率与正面向上的概率仍然都为0.5.故③正确.
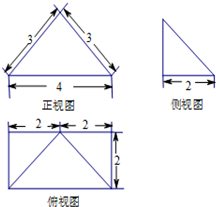
④已知四棱锥P-ABCD的直观图如图所示,
该几何体是底面为矩形,一侧面PCD垂直于底面ABCD的四棱锥,
S=S△PCD+2S△PBC+S△PAB=$\frac{1}{2}\sqrt{{3}^{2}-{2}^{2}}$×4+2×$\frac{1}{2}$×3×2+$\frac{1}{2}$×4×$\sqrt{{3}^{2}+{2}^{2}-{2}^{2}}$=12+2$\sqrt{5}$,故④正确.
故答案为:①③④
点评 本题以命题的真假判断与应用为载体,考查了系统抽样,函数的图象和性质,概率,棱锥的体积,难度中档.


 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案科目:高中数学 来源: 题型:选择题
| A. | 12种 | B. | 16种 | C. | 20种 | D. | 24种 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图所示,已知正方体(图1)面对角线长为a,沿对角面将其切割成两块,拼成图2所示的几何体,那么拼成后的几何体的全面积为$({2+\sqrt{2}}){a^2}$.
如图所示,已知正方体(图1)面对角线长为a,沿对角面将其切割成两块,拼成图2所示的几何体,那么拼成后的几何体的全面积为$({2+\sqrt{2}}){a^2}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-1)∪(2,+∞) | B. | (-1,2) | C. | (1,2) | D. | (2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
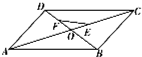
| A. | $\overrightarrow{FE}=-\frac{1}{12}\overrightarrow{AB}-\frac{1}{12}\overrightarrow{AD}$ | B. | $\overrightarrow{FE}=-\frac{1}{12}\overrightarrow{AB}-\frac{5}{12}\overrightarrow{AD}$ | C. | $\overrightarrow{FE}=\frac{5}{12}\overrightarrow{AB}-\frac{1}{12}\overrightarrow{AD}$ | D. | $\overrightarrow{FE}=\frac{5}{12}\overrightarrow{AB}-\frac{5}{12}\overrightarrow{AD}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 用若干块相同的小正方体搭成一个几何体,从两个角度观察得到的图形,则搭成该几何体最少需要的小正方体的块数是( )块?
用若干块相同的小正方体搭成一个几何体,从两个角度观察得到的图形,则搭成该几何体最少需要的小正方体的块数是( )块?| A. | 8 | B. | 7 | C. | 6 | D. | 5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com