
【题目】从2016年1月1日起全国统一实施全面两孩政策. 为了解适龄民众对放开
生二胎政策的态度,某市选取70后作为调查对象,随机调查了10人,其中打算生二胎
的有4人,不打算生二胎的有6人.
(1)从这10人中随机抽取3人,记打算生二胎的人数为![]() ,求随机变量
,求随机变量![]() 的分布列和数学期望;
的分布列和数学期望;
(2)若以这10人的样本数据估计该市的总体数据,且以频率作为概率,从该市70后中随机抽取3人,记打算生二胎的人数为![]() ,求随机变量
,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
科目:高中数学 来源: 题型:
【题目】【选做题】本题包括A、B、C、D四小题,请选定其中两小题,并在相应的答题区域内作答.若多做,则按作答的前两小题评分.解答时应写出文字说明、证明过程或演算步骤.
A.[选修4-1:几何证明选讲]
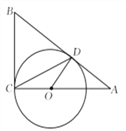
如图, ![]() 分别与圆
分别与圆![]() 相切于点
相切于点![]() ,
, ![]() ,
, ![]() 经过圆心
经过圆心![]() ,且
,且![]() ,求证:
,求证: ![]() .
.
B.[选修4-2:矩阵与变换]
在平面直角坐标系中,已知点![]() ,
, ![]() ,
, ![]() ,
, ![]() ,先将正方形
,先将正方形![]() 绕原点
绕原点![]() 逆时针旋转
逆时针旋转![]() ,再将所得图形的纵坐标压缩为原来的一半、横坐标不变,求连续两次变换所对应的矩阵
,再将所得图形的纵坐标压缩为原来的一半、横坐标不变,求连续两次变换所对应的矩阵![]() .
.
C.[选修4-4:坐标系与参数方程]
在平面直角坐标系![]() 中,已知曲线
中,已知曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).现以
为参数).现以![]() 为极点,
为极点, ![]() 轴的正半轴为极轴,建立极坐标系,求曲线
轴的正半轴为极轴,建立极坐标系,求曲线![]() 的极坐标方程.
的极坐标方程.
D.[选修4-5:不等式选讲]
已知![]() 为互不相等的正实数,求证:
为互不相等的正实数,求证: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
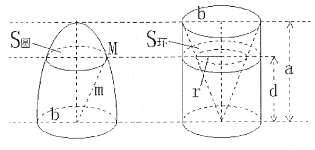
【题目】祖暅(公元前5-6世纪),祖冲之之子,是我国齐梁时代的数学家. 他提出了一条原理:“幂势既同,則积不容异. ”这句话的意思是:两个等高的几何体若在所有等高处的水平截面的面积相等,则这两个几何体的体积相等. 该原理在西方直到十七世纪才由意大利数学家卡瓦列利发现,比祖暅晚一千一百多年. 椭球体是椭圆绕其轴旋转所成的旋转体. 如图将底面直径皆为![]() ,高皆为
,高皆为![]() 的椭半球体及已被挖去了圆锥体的圆柱体放置于同一平面
的椭半球体及已被挖去了圆锥体的圆柱体放置于同一平面![]() 上. 以平行于平面
上. 以平行于平面![]() 的平面于距平面
的平面于距平面![]() 任意高
任意高![]() 处可横截得到
处可横截得到![]() 及
及![]() 两截面,可以证明
两截面,可以证明![]() 知总成立. 据此,短轴长为
知总成立. 据此,短轴长为![]() ,长轴为
,长轴为![]() 的椭球体的体积是 __________
的椭球体的体积是 __________![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某电子公司开发一种智能手机的配件,每个配件的成本是15元,销售价是20元,月平均销售![]() 件,通过改进工艺,每个配件的成本不变,质量和技术含金量提高,市场分析的结果表明,如果每个配件的销售价提高的百分率为
件,通过改进工艺,每个配件的成本不变,质量和技术含金量提高,市场分析的结果表明,如果每个配件的销售价提高的百分率为![]() ,那么月平均销售量减少的百分率为
,那么月平均销售量减少的百分率为![]() ,记改进工艺后电子公司销售该配件的月平均利润是
,记改进工艺后电子公司销售该配件的月平均利润是![]() (元).
(元).
(1)写出![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)改进工艺后,试确定该智能手机配件的售价,使电子公司销售该配件的月平均利润最大.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某农科所对冬季昼夜温差大小与某反季节大豆新品种发芽多少之间的关系进行分析研究,他们分别记录了12月1日至12月5日的每天昼夜温差与实验室每天每100颗种子中的发芽数,得到如下资料:
日期 | 12月1日 | 12月2日 | 12月3日 | 12月4日 | 12月5日 |
温差x (℃) | 10 | 11 | 13 | 12 | 8 |
发芽数y(颗) | 23 | 25 | 30 | 26 | 16 |
该农科所确定的研究方案是:先从这五组数据中选取2组,用剩下的3组数据求线性回归方程,再对被选取的2组数据进行检验.
(1)若选取的是12月1日与12月5日的两组数据,请根据12月2日至12月4日的数据,求出y关于x的线性回归方程![]() =
=![]() x+
x+![]() ;
;
(2)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2颗,则认为得到的线性回归方程是可靠的,试问(1)中所得的线性回归方程是否可靠?
附: 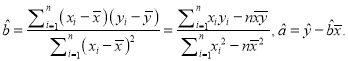
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】祖暅是南北朝时代的伟大科学家,5世纪末提出体积计算原理,即祖暅原理:“幂势既同,则积不容异”.意思是:夹在两个平行平面之间的两个几何体,被平行于这两个平面的任何一个平面所截,如果截面面积都相等,那么这两个几何体的体积一定相等.现有以下四个几何体:图①是从圆柱中挖出一个圆锥所得的几何体;图②、图③、图④分别是圆锥、圆台和半球,则满足祖暅原理的两个几何体为( )
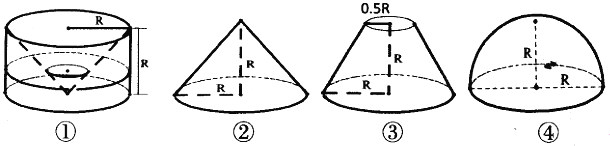
A. ①② B. ①③ C. ②④ D. ①④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() :
: ![]() ,定点
,定点![]() (常数
(常数![]() )的直线
)的直线![]() 与曲线
与曲线![]() 相交于
相交于![]() 、
、![]() 两点.
两点.
(1)若点![]() 的坐标为
的坐标为![]() ,求证:
,求证: ![]()
(2)若![]() ,以
,以![]() 为直径的圆的位置是否恒过一定点?若存在,求出这个定点,若不存在,请说明理由.
为直径的圆的位置是否恒过一定点?若存在,求出这个定点,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 的左顶点为
的左顶点为![]() ,右焦点为
,右焦点为![]() ,
, ![]() 为原点,
为原点, ![]() ,
, ![]() 是
是![]() 轴上的两个动点,且
轴上的两个动点,且![]() ,直线
,直线![]() 和
和![]() 分别与椭圆
分别与椭圆![]() 交于
交于![]() ,
, ![]() 两点.
两点.

(Ⅰ)求![]() 的面积的最小值;
的面积的最小值;
(Ⅱ)证明: ![]() ,
, ![]() ,
, ![]() 三点共线.
三点共线.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】三个臭皮匠顶上一个诸葛亮,能顶得上吗?在一次有关“三国演义”的知识竞赛中,三个臭皮匠A、B、C能答对题目的概率分别为P(A)=![]() ,P(B)=
,P(B)=![]() ,P(C)=
,P(C)=![]() ,诸葛亮D能答对题目的概率为P(D)=
,诸葛亮D能答对题目的概率为P(D)=![]() ,如果将三个臭皮匠A、B、C组成一组与诸葛亮D比赛,答对题目多者为胜方,问哪方胜?
,如果将三个臭皮匠A、B、C组成一组与诸葛亮D比赛,答对题目多者为胜方,问哪方胜?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com