
【题目】如图矩形![]() 中,
中, ![]() .点
.点![]() 在
在![]() 边上,
边上, ![]() 且
且![]() ,
, ![]() 沿直线
沿直线![]() 向上折起成
向上折起成![]() .记二面角
.记二面角![]() 的平面角为
的平面角为![]() ,当
,当![]()
![]() 时,
时,


①存在某个位置,使![]() ;
;
②存在某个位置,使![]() ;
;
③任意两个位置,直线![]() 和直线
和直线![]() 所成的角都不相等.
所成的角都不相等.
以上三个结论中正确的序号是
A. ① B. ①② C. ①③ D. ②③
【答案】C
【解析】对于①,当平面![]() 面
面![]() 时,
时, ![]() 面
面![]() ,故①正确;对于②,若存在某个位置,使
,故①正确;对于②,若存在某个位置,使![]() ,
, ![]() 面
面![]() 与
与![]() 为锐角相矛盾,
为锐角相矛盾, ![]() ②错误;对于③,设
②错误;对于③,设![]() 于
于![]() ,则
,则![]() 在以
在以![]() 为圆心以
为圆心以![]() 为半径的半圆上,且
为半径的半圆上,且![]() 与半圆所在的平面垂直,所以
与半圆所在的平面垂直,所以![]() 与半圆所在的圆为底面的圆锥母线成的角都相等,而直线
与半圆所在的圆为底面的圆锥母线成的角都相等,而直线![]() 任何位置都不是满足条件的圆锥的两条母线,所以任意两个位置,直线
任何位置都不是满足条件的圆锥的两条母线,所以任意两个位置,直线![]() 与
与![]() 所成的角都不相等,故③正确,故选C.
所成的角都不相等,故③正确,故选C.
【 方法点睛】本题主要通过对多个命题真假的判断,主要综合考查线面垂直的判定与性质、面面垂直的性质、异面直线所成的角以及空间想象能力与抽象思维能力,属于难题. 这种题型综合性较强,也是高考的命题热点,同学们往往因为某一处知识点掌握不好而导致“全盘皆输”,因此做这类题目更要细心、多读题,尽量挖掘出题目中的隐含条件,另外,要注意从简单的自己已经掌握的知识点入手,然后集中精力突破较难的命题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】若直线![]() 与曲线
与曲线![]() 满足下列两个条件:
满足下列两个条件:
(i)直线![]() 在点
在点![]() 处与曲线
处与曲线![]() 相切;(ii)曲线
相切;(ii)曲线![]() 在点
在点![]() 附近位于直线
附近位于直线![]() 的两侧.则称直线
的两侧.则称直线![]() 在点
在点![]() 处“切过”曲线
处“切过”曲线![]() .
.
下列命题正确的是__________(写出所有正确命题的编号).
①直线![]() 在点
在点![]() 处“切过”曲线
处“切过”曲线![]() ;
;
②直线![]() 在点
在点![]() 处“切过”曲线
处“切过”曲线![]() ;
;
③直线![]() 在点
在点![]() 处“切过”曲线
处“切过”曲线![]() ;
;
④直线![]() 在点
在点![]() 处“切过”曲线
处“切过”曲线![]() ;
;
⑤直线![]() 在点
在点![]() 处“切过”曲线
处“切过”曲线![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知以点A(-1,2)为圆心的圆与直线l1:x+2y+7=0相切.过点B(-2,0)的动直线l与圆A相交于M,N两点,Q是MN的中点.
(1)求圆A的方程;
(2)当|MN|=2![]() 时,求直线l的方程.
时,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知表1和表2是某年部分日期的天安门广场升旗时刻表:
表1:某年部分日期的天安门广场升旗时刻表
日期 | 升旗时刻 | 日期 | 升旗时刻 | 日期 | 升旗时刻 | 日期 | 升旗时刻 |
1月1日 | 7:36 | 4月9日 | 5:46 | 7月9日 | 4:53 | 10月8日 | 6:17 |
1月21日 | 7:11 | 4月28日 | 5:19 | 7月27日 | 5:07 | 10月26日 | 6:36 |
2月10日 | 7:14 | 5月16日 | 4:59 | 8月14日 | 5:24 | 11月13日 | 6:56 |
3月2日 | 6:47 | 6月3日 | 4:47 | 9月2日 | 5:42 | 12月1日 | 7:16 |
3月22日 | 6:15 | 6月22日 | 4:46 | 9月20日 | 5:50 | 12月20日 | 7:31 |
表2:某年1月部分日期的天安门广场升旗时刻表
日期 | 升旗时刻 | 日期 | 升旗时刻 | 日期 | 升旗时刻 |
2月1日 | 7:23 | 2月11日 | 7:13 | 2月21日 | 6:59 |
2月3日 | 7:22 | 2月13日 | 7:11 | 2月23日 | 6:57 |
2月5日 | 7:20 | 2月15日 | 7:08 | 2月25日 | 6:55 |
2月7日 | 7:17 | 2月17日 | 7:05 | 2月27日 | 6:52 |
2月9日 | 7:15 | 2月19日 | 7:02 | 2月28日 | 6:49 |
(1)从表1的日期中随机选出一天,试估计这一天的升旗时刻早于7:00的概率;
(2)甲、乙二人各自从表2的日期中随机选择一天观看升旗,且两人的选择相互独立,记![]() 为这两人中观看升旗的时刻早于7:00的人数,求
为这两人中观看升旗的时刻早于7:00的人数,求![]() 的 分布列和数学期望;
的 分布列和数学期望;
(3)将表1和表2的升旗时刻化为分数后作为样本数据(如7:31化为![]() ),记表2中所有升旗时刻对应数据的方差为
),记表2中所有升旗时刻对应数据的方差为![]() ,表1和表2中所有升旗时刻对应数据的方差为
,表1和表2中所有升旗时刻对应数据的方差为![]() ,判断
,判断![]() 与
与![]() 的大小(只需写出结论).
的大小(只需写出结论).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合![]() ,其中
,其中![]()
![]() .
. ![]() 表示
表示![]()
![]() 中所有不同值的个数.
中所有不同值的个数.
(Ⅰ)若集合![]() ,求
,求![]() ;
;
(Ⅱ)若集合![]() ,求证:
,求证: ![]() 的值两两不同,并求
的值两两不同,并求![]() ;
;
(Ⅲ)求![]() 的最小值.(用含
的最小值.(用含![]() 的代数式表示)
的代数式表示)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,飞镖的标靶呈圆盘形,圆盘被10等分,按如图所示染色为Ⅰ、Ⅱ、Ⅲ三部分,某人依次将若干支飞镖投向标靶,如果每次投射都是相互独立的.
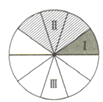
(1)如果他投向标靶的飞镖恰有2支且都击中标靶,同时每支飞镖击中标靶的任意位置都是等可能的,求“第Ⅰ部分被击中2次或第Ⅱ部分被击中2次”的概率;
(2)如果他投向标靶的飞镖恰有4支,且他投射1支飞镖,击中标靶的概率为![]() ,设
,设![]() 表示标靶被击中的次数,求
表示标靶被击中的次数,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校初三年级有![]() 名学生,随机抽查了
名学生,随机抽查了![]() 名学生,测试
名学生,测试![]() 分钟仰卧起坐的成绩(次数),将数据整理后绘制成如图所示的频率分布直方图.用样本估计总体,下列结论正确的是( )
分钟仰卧起坐的成绩(次数),将数据整理后绘制成如图所示的频率分布直方图.用样本估计总体,下列结论正确的是( )

A. 该校初三年级学生![]() 分钟仰卧起坐的次数的中位数为
分钟仰卧起坐的次数的中位数为![]() 次
次
B. 该校初三年级学生![]() 分钟仰卧起坐的次数的众数为
分钟仰卧起坐的次数的众数为![]() 次
次
C. 该校初三年级学生![]() 分钟仰卧起坐的次数超过
分钟仰卧起坐的次数超过![]() 次的人数约有
次的人数约有![]() 人
人
D. 该校初三年级学生![]() 分钟仰卧起坐的次数少于
分钟仰卧起坐的次数少于![]() 次的人数约为
次的人数约为![]() 人.
人.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C:x2+(y-a)2=4,点A(1,0).
(1)当过点A的圆C的切线存在时,求实数a的取值范围;
(2)设AM、AN为圆C的两条切线,M、N为切点,当MN=![]() 时,求MN所在直线的方程.
时,求MN所在直线的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com