
分析 (1)通过将点(b,$\frac{\sqrt{2}}{2}$b)代入椭圆方程,利用离心率的定义计算即得结论;
(2)通过(1)及椭圆C的短轴长为2可知椭圆C方程为:$\frac{{x}^{2}}{2}$+y2=1,通过令直线l1、l2方程中x=0可知yM=$\frac{\sqrt{2}{y}_{0}}{\sqrt{2}+{x}_{0}}$、yN=$\frac{\sqrt{2}{y}_{0}}{\sqrt{2}-{x}_{0}}$,进而利用切割线定理即得结论.
解答 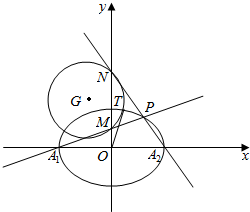 解:(1)依题意,$\frac{{b}^{2}}{{a}^{2}}$+$\frac{(\frac{\sqrt{2}}{2}b)^{2}}{{b}^{2}}$=1,
解:(1)依题意,$\frac{{b}^{2}}{{a}^{2}}$+$\frac{(\frac{\sqrt{2}}{2}b)^{2}}{{b}^{2}}$=1,
整理得:a=$\sqrt{2}$b,
∴椭圆C的离心率e=$\frac{c}{a}$=$\frac{\sqrt{{a}^{2}-{b}^{2}}}{a}$=$\frac{\sqrt{{a}^{2}-\frac{1}{2}{a}^{2}}}{a}$=$\frac{\sqrt{2}}{2}$;
(2)∵椭圆C的短轴长为2,
∴b=1,
又∵a=$\sqrt{2}$b,
∴a=$\sqrt{2}$,
∴椭圆C方程为:$\frac{{x}^{2}}{2}$+y2=1,
∴A1(-$\sqrt{2}$,0)、A2($\sqrt{2}$,0),记P(x0,y0),
则直线l1方程为:y-0=$\frac{{y}_{0}-0}{{x}_{0}+\sqrt{2}}$(x+$\sqrt{2}$),
令x=0可知:yM=$\frac{\sqrt{2}{y}_{0}}{\sqrt{2}+{x}_{0}}$;
直线l2方程为:y-0=$\frac{{y}_{0}-0}{{x}_{0}-\sqrt{2}}$(x-$\sqrt{2}$),
令x=0可知:yN=$\frac{\sqrt{2}{y}_{0}}{\sqrt{2}-{x}_{0}}$;
则|OM|•|ON|=|$\frac{\sqrt{2}{y}_{0}}{\sqrt{2}+{x}_{0}}$•$\frac{\sqrt{2}{y}_{0}}{\sqrt{2}-{x}_{0}}$|=|$\frac{2{{y}_{0}}^{2}}{2-{{x}_{0}}^{2}}$|,
又∵$\frac{{{x}_{0}}^{2}}{2}$+${{y}_{0}}^{2}$=1,
∴${{y}_{0}}^{2}$=1-$\frac{{{x}_{0}}^{2}}{2}$,
∴$\frac{2{{y}_{0}}^{2}}{2-{{x}_{0}}^{2}}$=$\frac{2-{{x}_{0}}^{2}}{2-{{x}_{0}}^{2}}$=1,
由切割线定理可知|OT|2=|OM|•|ON|=1,
∴点T的轨迹是以坐标原点为圆心、1为半径的圆周.
点评 本题考查椭圆的简单性质,熟练掌握椭圆的标准方程及其性质、直线的方程、点在椭圆上满足的条件、切割线定理是解题的关键,注意解题方法的积累,属于中档题.


 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 在空间直角坐标系中有单位正方体ABCD-A′B′C′D′,E,F分别是棱C′D′和B′C′的中点,试求:
在空间直角坐标系中有单位正方体ABCD-A′B′C′D′,E,F分别是棱C′D′和B′C′的中点,试求:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1<m<4 | B. | -1<m<3 | C. | 1<m<4 | D. | 1<m<3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com