
【题目】如图所示,在四棱锥P﹣ABCD中,侧面PAD垂直底面ABCD,∠PAD=∠ABC![]() ,设
,设![]() .
.
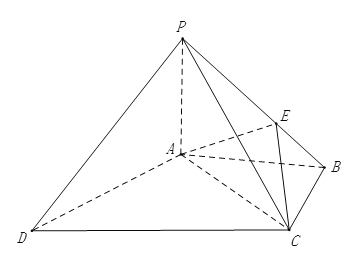
(1)求证:AE垂直BC;
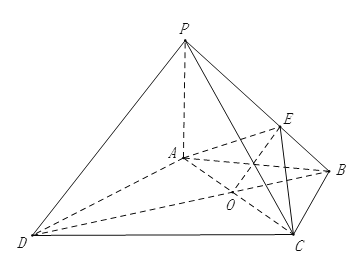
(2)若直线AB∥平面PCD,且DC=2AB,求证:直线PD∥平面ACE.
【答案】(1)证明见解析(2)证明见解析
【解析】
(1)先证明BC⊥平面PAB ,根据AE平面PAB得到证明。
(2)连结AC,BD,交于点O,连结OE,证明△ABO∽△CDO,根据相似得到OE∥PD,得到证明。
(1)∵在四棱锥P﹣ABCD中,∠PAD![]() ,∴PA⊥AD,
,∴PA⊥AD,
∵侧面PAD垂直底面ABCD,侧面PAD∩底面ABCD=AD,
∴PA⊥底面ABCD,∵BC平面ABCD,∴PA⊥BC,∵∠ABC![]() ,∴AB⊥BC,
,∴AB⊥BC,
∵PA∩AB=A,∴BC⊥平面PAB,∵AE平面PAB,∴AE垂直BC.
(2)连结AC,BD,交于点O,连结OE,
∵直线AB∥平面PCD,ABCD是平面图形,∴AB∥CD,
∴△ABO∽△CDO,
∵![]() ,且DC=2AB,∴
,且DC=2AB,∴![]() ,∴OE∥PD,
,∴OE∥PD,
∵OE平面ACE,PO平面ACE,∴直线PD∥平面ACE.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x3-3x2+1,g(x)=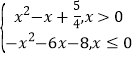 ,若方程g[f(x)]-a=0(a>0)有6个实数根(互不相同),则实数a的取值范围是______.
,若方程g[f(x)]-a=0(a>0)有6个实数根(互不相同),则实数a的取值范围是______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C的对边分别为a,b,c,且2ccosB=2a+b.
(1)求角C的大小;
(2)若△ABC的面积等于![]() ,求ab的最小值.
,求ab的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】通过随机询问100名性别不同的大学生是否爱好某项运动,得到如下![]() 列联表:
列联表:
(1)能否有![]() 的把握认为是否爱好该项运动与性别有关?请说明理由.
的把握认为是否爱好该项运动与性别有关?请说明理由.
(2)利用分层抽样的方法从以上爱好该项运动的大学生中抽取6人组建“运动达人社”,现从“运动达人社”中选派2人参加某项校际挑战赛,求选出的2人中恰有1名女大学生的概率.
男 | 女 | 总计 | |
爱好 | 40 | 20 | 60 |
不爱好 | 15 | 25 | 40 |
总计 | 55 | 45 | 100 |
附:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
 ,其中
,其中![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知不等式|x+1|>|2﹣x|+1的解集为M,且a,b,c∈M.
(1)比较|a﹣b|与|1﹣ab|的大小,并说明理由;
(2)若![]() ,求a2+b2+c2的最小值.
,求a2+b2+c2的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图的折线图是某超市2018年一月份至五月份的营业额与成本数据,根据该折线图,下列说法正确的是( )
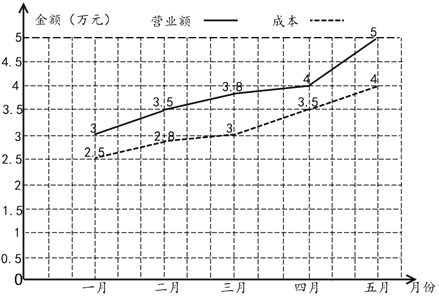
A.该超市2018年的前五个月中三月份的利润最高
B.该超市2018年的前五个月的利润一直呈增长趋势
C.该超市2018年的前五个月的利润的中位数为0.8万元
D.该超市2018年前五个月的总利润为3.5万元
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位40岁以上的女性职工共有60人,为了调查一下体重和年龄的关系,将这60人随机按1~60编号,用系统抽样的方法从中抽取10人,测量一下体重.
(1)若被抽出的号码其中一个为7,则最后被抽出的号码是多少?
(2)被抽取的10个人的体重(单位:![]() ),用茎叶图表示如图,求这10人体重的中位数与平均数;
),用茎叶图表示如图,求这10人体重的中位数与平均数;

(3)从这10个人中体重超过![]() 的人中随机抽取2人,参加健康指导培训,求体重为
的人中随机抽取2人,参加健康指导培训,求体重为![]() 的人被抽到的概率.
的人被抽到的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com