
【题目】已知函数f(x)=x2﹣cosx,x∈[﹣ ![]() ,
, ![]() ],则满足f(x0)>f(
],则满足f(x0)>f( ![]() )的x0的取值范围为 .
)的x0的取值范围为 .
【答案】[﹣ ![]() ,﹣
,﹣ ![]() )∪(
)∪( ![]() ,
,![]() ]
]
【解析】解:注意到函数f(x)=x2﹣cosx,x∈[﹣ ![]() ,
, ![]() ]是偶函数,
]是偶函数,
故只需考虑[0, ![]() ]区间上的情形.
]区间上的情形.
当x∈[0, ![]() ]时,f′(x)=2x+sinx≥0,
]时,f′(x)=2x+sinx≥0,
∴函数在[0, ![]() ]单调递增,
]单调递增,
所以f(x0)>f( ![]() )在[0,
)在[0, ![]() ]上的解集为(
]上的解集为( ![]() ,
, ![]() ],
],
结合函数是偶函数,图象关于y轴对称,
得原问题中x0取值范围是[﹣ ![]() ,﹣
,﹣ ![]() )∪(
)∪( ![]() ,
, ![]() ],
],
所以答案是:[﹣ ![]() ,﹣
,﹣ ![]() )∪(
)∪( ![]() ,
, ![]() ].
].
【考点精析】解答此题的关键在于理解利用导数研究函数的单调性的相关知识,掌握一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减.
在这个区间单调递减.


 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案科目:高中数学 来源: 题型:
【题目】已知向量![]() ,记
,记![]()
![]() .
.
(Ⅰ)求![]() 的单调递减区间;
的单调递减区间;
(Ⅱ)若![]() ,求
,求 ![]() 的值;
的值;
(Ⅲ)将函数![]() 的图象向右平移
的图象向右平移![]() 个单位得到
个单位得到![]() 的图象,若函数
的图象,若函数![]() 在
在![]() 上有零点,求实数
上有零点,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x+a|.
(1)若a=2,解关于x的不等式f(x)+f(x﹣3)≥5;
(2)若关于x的不等式f(x)﹣f(x+2)+4≥|1﹣3m|恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,四棱锥 ![]() 的底面为直角梯形,
的底面为直角梯形, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 底面
底面 ![]() ,
, ![]() 为
为 ![]() 的中点.
的中点.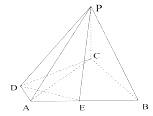
(Ⅰ)求证:平面 ![]() 平面
平面 ![]()
(Ⅱ)求直线 ![]() 与平面
与平面 ![]() 所成的角的正弦值.
所成的角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com