
(2015•兴国县一模)定义方程f(x)=f′(x)的实数根x0叫做函数f(x)的“新驻点”,若函数g(x)=x,h(x)=ln(x+1),φ(x)=x3﹣1的“新驻点”分别为α,β,γ,则α,β,γ的大小关系为( )
A.γ>α>β B.β>α>γ C.α>β>γ D.β>γ>α
A
【解析】
试题分析:分别对g(x),h(x),φ(x)求导,令g′(x)=g(x),h′(x)=h(x),φ′(x)=φ(x),
则它们的根分别为α,β,γ,即α=1,ln(β+1)=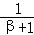 ,γ3﹣1=3γ2,然后分别讨论β、γ的取值范围即可.
,γ3﹣1=3γ2,然后分别讨论β、γ的取值范围即可.
【解析】
∵g′(x)=1,h′(x)=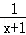 ,φ′(x)=3x2,
,φ′(x)=3x2,
由题意得:
α=1,ln(β+1)=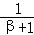 ,γ3﹣1=3γ2,
,γ3﹣1=3γ2,
①∵ln(β+1)=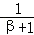 ,
,
∴(β+1)β+1=e,
当β≥1时,β+1≥2,
∴β+1≤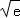 <2,
<2,
∴β<1,这与β≥1矛盾,
∴0<β<1;
②∵γ3﹣1=3γ2,且γ=0时等式不成立,
∴3γ2>0
∴γ3>1,
∴γ>1.
∴γ>α>β.
故答案为 A.


科目:高中数学 来源:[同步]2014年湘教版选修2-3 8.4列联表独立性分析案例练习卷(解析版) 题型:?????
(2013•江西一模)甲、乙两名棋手比赛正在进行中,甲必须再胜2盘才最后获胜,乙必须再胜3盘才最后获胜,若甲、乙两人每盘取胜的概率都是 ,则甲最后获胜的概率是( )
,则甲最后获胜的概率是( )
A.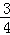 B.
B.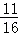 C.
C.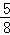 D.
D.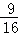
查看答案和解析>>
科目:高中数学 来源:[同步]2014年湘教版选修2-2 4.2导数的运算练习卷(解析版) 题型:?????
(2014•浙江模拟)已知f(x)为R上的可导函数,且满足f(x)>f′(x),对任意正实数a,下面不等式恒成立的是( )
A.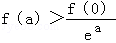
B.
C.f(a)>eaf(0)
D.f(a)<eaf(0)
查看答案和解析>>
科目:高中数学 来源:[同步]2014年湘教版选修2-2 4.2导数的运算练习卷(解析版) 题型:?????
(2014•重庆三模)对于三次函数f(x)=ax3+bx2+cx+d(a≠0),给出定义:设f′(x)是函数y=f(x)的导数,f″(x)是f′(x)的导数,若方程f′′(x)=0有实数解x0,则称点(x0,f(x0))为函数y=f(x)的“拐点”.某同学经过探究发现:任何一个三次函数都有“拐点”;任何一个三次函数都有对称中心,且“拐点”就是对称中心.设函数g(x)=
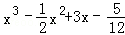 ,则g(
,则g(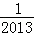 )+
)+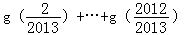 =( )
=( )
A.2011 B.2012 C.2013 D.2014
查看答案和解析>>
科目:高中数学 来源:[同步]2014年湘教版选修2-1 3.9共面与平行练习卷(解析版) 题型:?????
若平面α与β的法向量分别是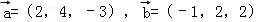 ,则平面α与β的位置关系是( )
,则平面α与β的位置关系是( )
A.平行 B.垂直 C.相交但不垂直 D.无法确定
查看答案和解析>>
科目:高中数学 来源:[同步]2014年湘教版选修2-1 3.9共面与平行练习卷(解析版) 题型:?????
已知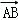 =(1,5,﹣2),
=(1,5,﹣2),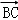 =(3,1,z),若
=(3,1,z),若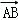 ⊥
⊥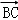 ,
,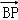 =(x﹣1,y,﹣3),且BP⊥平面ABC,则实数x、y、z分别为( )
=(x﹣1,y,﹣3),且BP⊥平面ABC,则实数x、y、z分别为( )
A.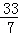 ,﹣
,﹣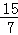 ,4 B.
,4 B.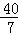 ,﹣
,﹣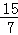 ,4 C.
,4 C.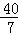 ,﹣2,4 D.4,
,﹣2,4 D.4,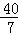 ,﹣15
,﹣15
查看答案和解析>>
科目:高中数学 来源:[同步]2014年湘教版选修2-1 3.5直线与平面的垂直关系练习卷(解析版) 题型:?????
(2012•资阳三模)△ABC和△DBC所在的平面相互垂直,且AB=BC=BD,∠CBA=∠DBC=120°,则AD和平面BCD所成的角为( )
A.30° B.45° C.60° D.90°
查看答案和解析>>
科目:高中数学 来源:[同步]2014年湘教版选修2-1 3.2空间中向量的概念和运算练习卷(解析版) 题型:?????
设平面α的一个法向量为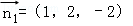 ,平面β的一个法向量为
,平面β的一个法向量为 ,若α∥β,则k=( )
,若α∥β,则k=( )
A.2 B.﹣4 C.﹣2 D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com