
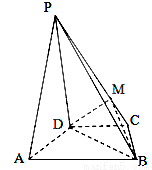
(本小题满分12分)如图,在四棱锥 中,平面
中,平面 平面
平面 ,
, ∥
∥
 ,已知
,已知


(1)设 是
是 上的一点,求证:平面
上的一点,求证:平面 平面
平面 ;
;
(2)当三角形 为正三角形时,点
为正三角形时,点 在线段
在线段 (不含线段端点)上的什么位置时,二面角
(不含线段端点)上的什么位置时,二面角 的大小为
的大小为
(1)证明如下;(2) 时符合条件;
时符合条件;
【解析】
试题分析:(1)考查面面垂直的判定定理,一条线垂直平面中两条相交的线,则线面平行,经过这条线的任何一个平面,都与该平面垂直;(2)考查二面角的问题,二面角是高中数学的一个难点,部分同学二面角问题的解决毫无头绪,再用立体几何知识解决此类问题,首先我们要判断好哪个角是二面角,在用空间向量解决此类问题时,判断二面角显得简单了许多,只要我们选取好法向量即可,对于本题,法向量为 ,
, ,再代入到数量积公式即可。
,再代入到数量积公式即可。
试题解析:(1)因为 ,得
,得 ,又因为
,又因为 ,所以有
,所以有 即
即 又因为平面
又因为平面 平面
平面 ,且交线为AD,所以
,且交线为AD,所以 ,
,
 ,故平面
,故平面 平面
平面 。。。。。。。。。。。。。。。4分
。。。。。。。。。。。。。。。4分
(2)由条件可知,三角形PAD为正三角形,所以取AD的中点O,连PO,则PO垂直于AD,
由于平面 平面
平面 ,所以PO垂直于平面ABCD,过O点作BD的平行线,交AB于点E,则有
,所以PO垂直于平面ABCD,过O点作BD的平行线,交AB于点E,则有 ,所以分别以
,所以分别以 为
为 轴,建空间直角坐标系
轴,建空间直角坐标系
所以点 ,由于
,由于 且
且 ,得到
,得到 ,
,
设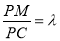 (
(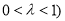 ,则有
,则有 ,因为由(1)的证明可知
,因为由(1)的证明可知 ,所以平面PAD的法向量可取:
,所以平面PAD的法向量可取: ,设平面MAD的法向量为
,设平面MAD的法向量为 ,则有
,则有 即有
即有
由二面角 成
成 得
得 ,故当M满足:
,故当M满足: 时符合条件。。。。。。。。。12分
时符合条件。。。。。。。。。12分
考点:?面面平行的判定定理?平面法向量的求法?数量积公式


科目:高中数学 来源:2015届云南省等校高三12月份统一考试文科数学试卷(解析版) 题型:选择题
阅读如图的程序框图,运行相应的程序,若输入x的值为﹣4,则输出y的值为( )

A.0.5 B.1 C.2 D.4
查看答案和解析>>
科目:高中数学 来源:2015届上海市高三上学期期中考试数学试卷(解析版) 题型:填空题
定义: 表示
表示 两个数中的最大值,
两个数中的最大值, 表示
表示 两个数中的最小值。给出下列4个命题:
两个数中的最小值。给出下列4个命题:
①
 且
且 ;
;
②
 且
且 ;
;
③设函数 和
和 的公共定义域为
的公共定义域为 ,若
,若 ,
, 恒成立,则
恒成立,则 ;
;
④若函数 的图像关于直线
的图像关于直线 对称,则
对称,则 的值为
的值为 。
。
其中真命题是 。(写出所有真命题的序号)
查看答案和解析>>
科目:高中数学 来源:2014-2015学年黑龙江省高二上学期期中理科数学试卷(解析版) 题型:填空题
设直线 与双曲线
与双曲线 的两条渐近线分别交于点
的两条渐近线分别交于点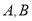 ,若点
,若点 满足
满足 ,则该双曲线的离心率是________.
,则该双曲线的离心率是________.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年黑龙江省高二上学期期中理科数学试卷(解析版) 题型:选择题
如图, 是直三棱柱,
是直三棱柱, ,点
,点 和
和 分别是
分别是 和
和 的中点,若
的中点,若
 ,则
,则 与
与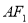 所成角的余弦值是( )
所成角的余弦值是( )
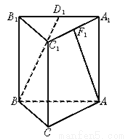
A. B.
B.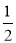 C.
C. D.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com