已知定义在R上的函数f(x)=ax3-3x,a为常数,且x=1是函数f(x)的一个极值点.
(Ⅰ)求a的值;
(Ⅱ)若函数g(x)=f(x)+f'(x)-6,x∈R,求g(x)的单调区间;
(Ⅲ) 过点A(1,m)(m≠-2)可作曲线y=f(x)的三条切线,求m的取值范围.
【答案】
分析:(Ⅰ)求出函数的导数,利用f′(1)=0,求出a的值;
(Ⅱ)通过函数g(x)=f(x)+f′(x)-6,x∈R,求出g(x)的表达式,通过函数的导数,利用导数为0,求出函数的单调区间;
(Ⅲ) 利用 f′(x)=3(x
2-1),设切点为T(x
,y
),则切线的斜率相等,方程有3个解,就是函数有2个极值点,并且极大值大于0,极小值小于0,即可求m的取值范围.
解答:解:(Ⅰ)f′(x)=3(ax
2-1),x=1是函数f(x)的一个极值点,则f′(1)=0,
∴a-1=0,∴a=1.
又f'(x)=3(x+1)(x-1),函数f(x)在x=1两侧的导数异号,
∴a=1.…(2分)
(Ⅱ)由(Ⅰ)知,g(x)=f(x)+f′(x)-6=x
3+3x
2-3x-9.
则g′(x)=3(x
2+2x-1),令g′(x)=0,得x
2+2x-1=0,∴
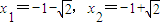
.
随x的变化,g′(x)与g(x)的变化如下:
所以函数g(x)的单调增区间为
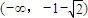
和
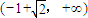
,单调减区间为
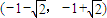
.…(8分)
(Ⅲ) f′(x)=3(x
2-1),设切点为T(x
,y
),则切线的斜率为
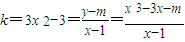
,…(9分)
整理得2x
3-3x
2+m+3=0,依题意,方程有3个根.…(10分)
设h(x)=2x
3-3x
2+m+3,则h′(x)=6x
2-6x=6x(x-1).
令h′(x)=0,得x
1=0,x
2=1,则h(x)在区间(-∞,0),[1,+∞)上单调递增,
在区间(0,1)上单调递减.…(11分)
因此,
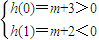
,解得-3<m<-2.所以m的取值范围为(-3,-2).…(14分)
点评:本题是难题,考查函数的导数的应用,极值的处理方法,切线的斜率与导数的函数值的关系,考查逻辑推理能力,分析问题解决问题的能力,计算量大,考查函数与方程的思想,转化思想,常考题型.

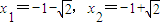 .
.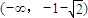
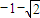
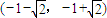
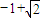
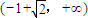
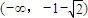 和
和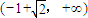 ,单调减区间为
,单调减区间为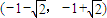 .…(8分)
.…(8分)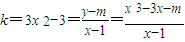 ,…(9分)
,…(9分)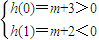 ,解得-3<m<-2.所以m的取值范围为(-3,-2).…(14分)
,解得-3<m<-2.所以m的取值范围为(-3,-2).…(14分)

 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案