
分析 由条件利用二项式定理求得代数式($\root{6}{x}$+$\frac{1}{\root{6}{x}}$)n的展开式.
解答 解:代数式($\root{6}{x}$+$\frac{1}{\root{6}{x}}$)n =${C}_{n}^{0}$•${x}^{\frac{n}{6}}$+${C}_{n}^{1}$•${x}^{\frac{n-1}{6}}$•${x}^{\frac{1}{6}}$+${C}_{n}^{2}$•${x}^{\frac{n-2}{6}}$•${x}^{-\frac{2}{6}}$+…+${C}_{n}^{n}$•${x}^{-\frac{n}{6}}$
${C}_{n}^{0}$•${x}^{\frac{n}{6}}$+${C}_{n}^{1}$•${x}^{\frac{n-2}{6}}$+${C}_{n}^{2}$•${x}^{\frac{n-4}{6}}$+…+${C}_{n}^{n}$•${x}^{-\frac{n}{6}}$.
点评 本题主要考查二项式定理的应用,二项展开式的通项公式,属于基础题.


 考前必练系列答案
考前必练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
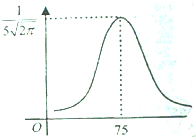 某市高二理科学生数学考试的成绩x服从正态分布,其密度函数为f(x)=$\frac{1}{\sqrt{2π}σ}$e${\;}^{\frac{(x-μ)^{2}}{2{σ}^{2}}}$,密度曲线如图,已知该市理科学生总数是10000人,则成绩位于(65,85]的人数约是9544.
某市高二理科学生数学考试的成绩x服从正态分布,其密度函数为f(x)=$\frac{1}{\sqrt{2π}σ}$e${\;}^{\frac{(x-μ)^{2}}{2{σ}^{2}}}$,密度曲线如图,已知该市理科学生总数是10000人,则成绩位于(65,85]的人数约是9544.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 68.26% | B. | 95.44% | C. | 99.74% | D. | 31.74% |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com