
分析 由已知结合同角三角函数的基本关系式求得$si{n}^{2}α=\frac{27}{35},si{n}^{2}β=\frac{3}{35}$,把$\frac{sin2α}{sin2β}$+$\frac{cos2α}{cos2β}$展开倍角公式后代值求得答案.
解答 解:∵$\frac{sinα}{sinβ}$=3,$\frac{cosα}{cosβ}$=$\frac{1}{2}$,∴sinα=3sinβ,cosβ=2cosα,
又sin2α+cos2α=1,sin2β+cos2β=1,解得:$si{n}^{2}α=\frac{27}{35},si{n}^{2}β=\frac{3}{35}$.
则$\frac{sin2α}{sin2β}$+$\frac{cos2α}{cos2β}$=$\frac{2sinαcosα}{2sinβcosβ}$$+\frac{1-2si{n}^{2}α}{1-2si{n}^{2}β}$
=$\frac{2•3sinβcosα}{2sinβ•2cosα}$+$\frac{1-2×\frac{27}{35}}{1-2×\frac{3}{35}}$
=$\frac{3}{2}-\frac{19}{29}=\frac{49}{58}$.
故答案为:$\frac{49}{58}$.
点评 本题考查同角三角函数的基本关系式,考查了二倍角公式,考查计算能力,是中档题.


 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案科目:高中数学 来源: 题型:选择题
| A. | 8 | B. | 12 | C. | $\frac{2}{9}$ | D. | 16 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{6}$ | B. | $\frac{1}{12}$ | C. | $\frac{1}{19}$ | D. | $\frac{1}{21}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
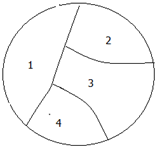 用五种不同的颜色给图中的四个区域涂色,每个区域涂一种颜色.
用五种不同的颜色给图中的四个区域涂色,每个区域涂一种颜色.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在四棱锥P-ABCD中,底面ABCD为平行四边形,∠DBA=30°,∠DAB=60°,AD=1,PD⊥底面ABCD.
如图,在四棱锥P-ABCD中,底面ABCD为平行四边形,∠DBA=30°,∠DAB=60°,AD=1,PD⊥底面ABCD.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com