Question

6．已知函数f（x）=$\left\{\begin{array}{l}{x，x＜1}\\{2x-1，1≤x＜10}\\{{3}^{x}-11，x≥10}\end{array}\right.$试设计算法及程序框图，并写出程序．要求输入自变量x，输出函数值．

Answer 1

分析 本题考查的知识点是设计程序框图解决实际问题，我们根据题目已知中分段函数的解析式，然后根据分类标准，设置两个判断框的并设置出判断框中的条件，再由函数各段的解析式，确定判断框的“是”与“否”分支对应的操作，由此即可画出流程图，再编写满足题意的程序．

解答 解：（解法1）算法如下：
第一步，输入x；                                    …（1分）
第二步，判断条件x＜1是否成立，若成立，则y=x，然后执行第四步，
否则，执行第三步；                          …（2分）
第三步，判断条件x＜10是否成立，若成立，则计算y=2x-1，
否则，计算y=3^x-11；                    …（3分）
第四步，输出y，结束算法．                         …（4分）
说明：若在第二步中，没有写“执行第四步”，扣（1分）．
（解法2）算法如下：
第一步，输入x；                                     …（1分）
第二步，判断条件x＜1是否成立，若成立，则y=x，
否则，执行第三步；                           …（2分）
第三步，判断条件1≤x＜10是否成立，若成立，则计算yt=2x-1，
否则，执行第四步；                           …
第四步，判断条件x≥10是否成立，若成立，则计算y=3^x-11，
否则，执行第五步；                           …（3分）
第五步，输出y，结束算法．                           …（4分）
（解法3）算法如下：
第一步，输入x；                     …（1分）
第二步，判断条件x＜1是否成立，若成立，则y=x，并输出y，结束算法；
否则，执行第三步；            …（2分）
第三步，判断条件x＜10是否成立，若成立，则计算y=2x-1，并输出y，
结束算法；否则，计算y=3^x-11，并输出y，结束算法…（4分）
说明：1．若在第二步中，没有写“结束算法”，扣（1分）；没有写“输出y”，合计扣（1分）；
框图
 
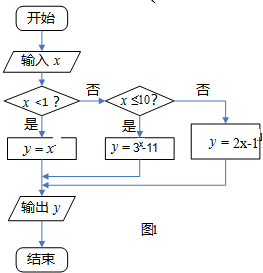
程序：
INPUT x
IF x＜1 THEN
  y=x
ELSE
   IF x＜=10 THEN
   y=2x-1   
   ELSE
   y=3∧x-11
   END IF
END IF
PRINT y
END

点评 本题考查了设计程序框图解决实际问题，主要考查编写程序解决分段函数问题．