
已知 ,函数
,函数 .
.

(1)当 时,画出函数
时,画出函数 的大致图像;
的大致图像;
(2)当 时,根据图像写出函数
时,根据图像写出函数 的单调减区间,并用定义证明你的结论;
的单调减区间,并用定义证明你的结论;
(3)试讨论关于x的方程 解的个数.
解的个数.
(1)详见解析;(2)详见解析;(3)详见解析.
【解析】
试题分析:(1)当a=2时,  ,作出图象;
,作出图象;
(2)由(1)写出函数y=f(x)的单调递增区间,再根据单调性定义证明即可;
(3)由题意知方程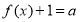 的解得个数等价于函数
的解得个数等价于函数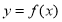 的图像与直线
的图像与直线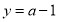 的交点个数.即函数
的交点个数.即函数 的图象与直线
的图象与直线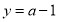 的交点个数.
的交点个数.
试题解析:(1)如图所示
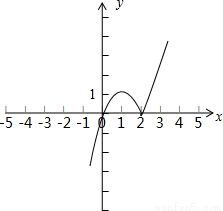 3分
3分
(2)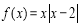 单调递减区间:
单调递减区间: 4分
4分
证明:设任意的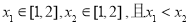
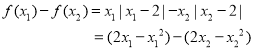
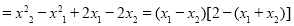 5分
5分
因为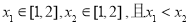 ,所以
,所以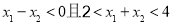
于是 ,即
,即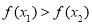 6分
6分
所以函数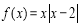 在
在 上是单调递减函数 7分
上是单调递减函数 7分
(3) 由题意知方程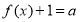 的解得个数等价于函数
的解得个数等价于函数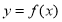 的图像与直线
的图像与直线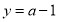 的交点个数.即函数
的交点个数.即函数 的图象与直线
的图象与直线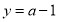 的交点个数
的交点个数
又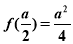 ,注意到
,注意到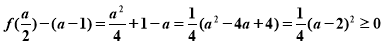 ,
,
当且仅当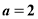 时,上式等号成立,借助图像知 8分
时,上式等号成立,借助图像知 8分
所以,当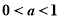 时,函数
时,函数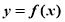 的图像与直线
的图像与直线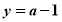 有1个交点; 9分
有1个交点; 9分
当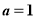 ,
,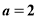 时,函数
时,函数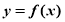 的图像与直线
的图像与直线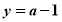 有2个交点; 10分
有2个交点; 10分
当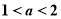 ,
,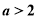 时,函数
时,函数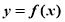 的图像与直线
的图像与直线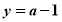 有3个交点;12分.
有3个交点;12分.
考点:1.绝对值的函数;2.函数的值域;3.函数的零点.


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:高中数学 来源:2015届辽宁省沈阳市高二质量监测理科数学试卷(解析版) 题型:填空题
在等差数列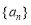 中,当
中,当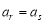
 时,
时,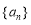 必定是常数数列.然而在等比数列
必定是常数数列.然而在等比数列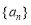 中,对某些正整数r、s
中,对某些正整数r、s ,当
,当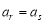 时,
时,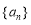 可以不是常数列,写出非常数数列
可以不是常数列,写出非常数数列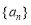 的一个通项公式 .
的一个通项公式 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com