
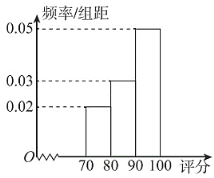
【题目】某歌手大赛进行电视直播,比赛现场有6名特约嘉宾给每位参赛选手评分,场内外的观众可以通过网络平台给每位参赛选手评分.某选手参加比赛后,现场嘉宾评分情况如下表;场内外共有数万名观众参与了评分,组织方将观众评分按照![]() ,
,![]() ,
,![]() 分组,绘成频率分布直方图如下:
分组,绘成频率分布直方图如下:
嘉宾 |
|
|
|
|
|
|
评分 | 96 | 95 | 96 | 89 | 97 | 98 |
(1)从观众中任取三人,求这三人中恰有1人分数在![]() 另2人分数在
另2人分数在![]() 的概率;
的概率;
(2)从嘉宾中随机选3人,记3人中分数不低于96分的人数为![]() ,求
,求![]() 的期望;
的期望;
(3)嘉宾评分的平均数为![]() ,场内外的观众评分的平均数为
,场内外的观众评分的平均数为![]() 与
与![]() 的大小关系(不需要证明).
的大小关系(不需要证明).
【答案】(1)![]() ; (2)2; (3)嘉宾的平均分高于观众的平均分.
; (2)2; (3)嘉宾的平均分高于观众的平均分.
【解析】
(1)根据频率分布直方图,即可求解![]() 内的概率和在
内的概率和在![]() 的概率;
的概率;
(2)由题意,得到从嘉宾中随机去3人,分数不低于96分的人数为![]() 的可能取值为
的可能取值为![]() ,求得相应的概率,得到随机变量的分布列,利用期望的公式,即可求解;
,求得相应的概率,得到随机变量的分布列,利用期望的公式,即可求解;
可得![]() ,
,
(3)利用平均数的计算公式和频率分布直方图的平均数的计算方法,分别求得![]() 的值,即可得到结论.
的值,即可得到结论.
(1)由题意,根据频率分布直方图可得,在![]() 内的概率为
内的概率为![]() ,在
,在![]() 的概率为
的概率为![]() ,所以概率
,所以概率![]() .
.
(2)由题意,6名特约嘉宾中,其中4人的得分不低于96分,2人的得分低于96分,
所以从嘉宾中随机选3人,分数不低于96分的人数为![]() 的可能取值为
的可能取值为![]() ,
,
可得![]() ,
,
所以随机变量![]() 的分布列为:
的分布列为:
| 1 | 2 | 3 |
|
|
|
|
所以期望为![]() .
.
(3)由表格中的数据可得,嘉宾的平均数为![]() ,
,
观众的平均得分为![]() ,
,
所以![]() ,即嘉宾的平均分高于观众的平均分.
,即嘉宾的平均分高于观众的平均分.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知数列![]() 满足:对任意的
满足:对任意的![]() ,若
,若![]() ,则
,则![]() ,且
,且![]() ,设集合
,设集合![]() ,集合
,集合![]() 中元素最小值记为
中元素最小值记为![]() ,集合
,集合![]() 中元素最大值记为
中元素最大值记为![]() .
.
(1)对于数列:![]() ,写出集合
,写出集合![]() 及
及![]() ;
;
(2)求证:![]() 不可能为18;
不可能为18;
(3)求![]() 的最大值以及
的最大值以及![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=sin(wx+![]() )(w>0,
)(w>0,![]() <
<![]() )的最小正周期是π,若将该函数的图象向右平移
)的最小正周期是π,若将该函数的图象向右平移![]() 个单位后得到的函数图象关于直线x=
个单位后得到的函数图象关于直线x=![]() 对称,则函数f(x)的解析式为( )
对称,则函数f(x)的解析式为( )
A.f(x)=sin(2x+![]() )B.f(x)=sin(2x-
)B.f(x)=sin(2x-![]() )
)
C.f(x)=sin(2x+![]() )D.f(x)=sin(2x-
)D.f(x)=sin(2x-![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从甲、乙两种树苗中各抽测了10株树苗的高度,其茎叶图如图.根据茎叶图,下列描述正确的是( )
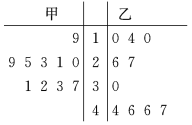
A.甲种树苗的平均高度大于乙种树苗的平均高度,且甲种树苗比乙种树苗长得整齐
B.甲种树苗的平均高度大于乙种树苗的平均高度,但乙种树苗比甲种树苗长得整齐
C.乙种树苗的平均高度大于甲种树苗的平均高度,且乙种树苗比甲种树苗长得整齐
D.乙种树苗的平均高度大于甲种树苗的平均高度,但甲种树苗比乙种树苗长得整齐
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年末,武汉出现新型冠状病毒肺炎(![]() )疫情,并快速席卷我国其他地区,传播速度很快.因这种病毒是以前从未在人体中发现的冠状病毒新毒株,所以目前没有特异治疗方法,防控难度很大.武汉市出现疫情最早,感染人员最多,防控压力最大,武汉市从2月7日起举全市之力入户上门排查确诊的新冠肺炎患者、疑似的新冠肺炎患者、无法明确排除新冠肺炎的发热患者和与确诊患者的密切接触者等“四类”人员,强化网格化管理,不落一户、不漏一人.在排查期间,一户6口之家被确认为“与确诊患者的密切接触者”,这种情况下医护人员要对其家庭成员随机地逐一进行“核糖核酸”检测,若出现阳性,则该家庭为“感染高危户”.设该家庭每个成员检测呈阳性的概率均为
)疫情,并快速席卷我国其他地区,传播速度很快.因这种病毒是以前从未在人体中发现的冠状病毒新毒株,所以目前没有特异治疗方法,防控难度很大.武汉市出现疫情最早,感染人员最多,防控压力最大,武汉市从2月7日起举全市之力入户上门排查确诊的新冠肺炎患者、疑似的新冠肺炎患者、无法明确排除新冠肺炎的发热患者和与确诊患者的密切接触者等“四类”人员,强化网格化管理,不落一户、不漏一人.在排查期间,一户6口之家被确认为“与确诊患者的密切接触者”,这种情况下医护人员要对其家庭成员随机地逐一进行“核糖核酸”检测,若出现阳性,则该家庭为“感染高危户”.设该家庭每个成员检测呈阳性的概率均为![]() (
(![]() )且相互独立,该家庭至少检测了5个人才能确定为“感染高危户”的概率为
)且相互独立,该家庭至少检测了5个人才能确定为“感染高危户”的概率为![]() ,当
,当![]() 时,
时,![]() 最大,则
最大,则![]() ( )
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,四棱锥![]() 中,侧面
中,侧面![]() 底面
底面![]() ,底面
,底面![]() 是平行四边形,
是平行四边形,![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 中点,点
中点,点![]() 在线段
在线段![]() 上.
上.
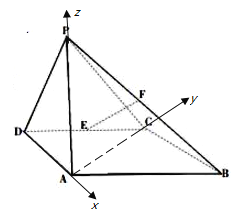
(Ⅰ)证明:![]() ;
;
(Ⅱ)若![]()
![]()
![]()
![]() ,求实数
,求实数![]() 使直线
使直线![]() 与平面
与平面![]() 所成角和直线
所成角和直线![]() 与平面
与平面![]() 所成角相等.
所成角相等.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设圆![]() 的圆心为
的圆心为![]() ,直线
,直线![]() 过点
过点![]() 且与
且与![]() 轴不重合,交圆
轴不重合,交圆![]() 于
于![]() ,
,![]() 两点,过点
两点,过点![]() 作
作![]() 的平行线交
的平行线交![]() 于点
于点![]() .
.
(1)求![]() 的值;
的值;
(2)设点![]() 的轨迹为曲线
的轨迹为曲线![]() ,直线
,直线![]() 与曲线
与曲线![]() 相交于
相交于![]() ,
,![]() 两点,与直线
两点,与直线![]() 相交于
相交于![]() 点,试问在椭圆
点,试问在椭圆![]() 上是否存在一定点
上是否存在一定点![]() ,使得
,使得![]() ,
,![]() ,
,![]() 成等差数列(其中
成等差数列(其中![]() ,
,![]() ,
,![]() 分别指直线
分别指直线![]() ,
,![]() ,
,![]() 的斜率).若存在,求出
的斜率).若存在,求出![]() 点的坐标;若不存在,请说明理由.
点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“割圆术”是刘徽最突出的数学成就之一,他在《九章算术注》中提出割圆术,并作为计算圆的周长,面积已经圆周率的基础,刘徽把圆内接正多边形的面积一直算到了正3072边形,并由此而求得了圆周率为3.1415和3.1416这两个近似数值,这个结果是当时世界上圆周率计算的最精确数据.如图,当分割到圆内接正六边形时,某同学利用计算机随机模拟法向圆内随机投掷点,计算得出该点落在正六边形内的频率为0.8269,那么通过该实验计算出来的圆周率近似值为(参考数据:![]() )
)

A. 3.1419B. 3.1417C. 3.1415D. 3.1413
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com