练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】如图，在道路边安装路灯，路面宽，灯柱高14，灯杆与地面所成角为30°．路灯采用锥形灯罩，灯罩轴线与灯杆垂直，轴线，灯杆都在灯柱和路面宽线确定的平面内．

    （1）当灯杆长度为多少时，灯罩轴线正好通过路面的中线?

    （2）如果灯罩轴线AC正好通过路面的中线，此时有一高2.5 的警示牌直立在处，求警示牌在该路灯灯光下的影子长度．

    【答案】（1）见解析；（2）见解析

    【解析】

    (1)分别以图中所在直线为轴，建立平面直角坐标系，分别计算AB，AC的直线方程，解得A坐标，求得AB长度.

    (2) 设警示牌为，，计算M，A的坐标，得到AM直线方程，得到答案.

    解：分别以图中所在直线为轴，建立平面直角坐标系，

    （1）【解法1】作垂足为，作垂足为

    因为灯杆与地面所成角为，即

    在中，

    所以在中，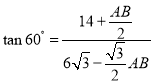

    解得：

    【解法2】

    灯杆与地面所成角为，，方程为①

    因为灯罩轴线与灯杆垂直，设的斜率为，所以，又因为

    的方程为：②

    联立：①②，解得：

    所以

    （2）设警示牌为，，则

    令，所以，所以

    答：（1）当灯杆长度为时，灯罩轴线正好通过路面的中线

    （2）求警示牌在该路灯灯光下的影子长度

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知数列{an}的前n项和Sn ， 若an+1+（﹣1）nan=n，则S40= ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知表1是某年部分日期的天安门广场升旗时刻表．

    表1：某年部分日期的天安门广场升旗时刻表

    将表1中的升旗时刻化为分数后作为样本数据（如：可化为）．

    （Ⅰ）请补充完成下面的频率分布表及频率分布直方图；

    分组

    频数

    频率

    4:00—4:59

    3

    5:00—5:59

    0.25

    6:00—6:59

    7:00—7:59

    5

    合计

    20

    （Ⅱ）若甲学校从上表日期中随机选择一天观看升旗．试估计甲学校观看升旗的时刻早于6:00的概率；

    （Ⅲ）若甲，乙两个学校各自从表1中五月、六月的日期中随机选择一天观看升旗, 求两校观看升旗的时刻均不早于5:00的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知边长为的正的顶点在平面内，顶点，在平面外的同一侧，点，分别为，在平面内的投影，设，直线与平面所成的角为.若是以角为直角的直角三角形，则的最小值为__________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在四面体中，平面平面，，，分别为的中点．

    （1）证明：平面平面；

    （2）求三棱锥的体积；

    （3）求二面角的大小．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图所示，近日我渔船编队在岛周围海域作业，在岛的南偏西20°方向有一个海面观测站，某时刻观测站发现有不明船只向我渔船编队靠近，现测得与相距31海里的处有一艘海警船巡航，上级指示海警船沿北偏西40°方向，以40海里/小时的速度向岛直线航行以保护我渔船编队，30分钟后到达处，此时观测站测得间的距离为21海里．

    (Ⅰ)求的值；

    (Ⅱ)试问海警船再向前航行多少分钟方可到岛？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在四面体ABCD中，若AB=CD= ，AC=BD=2，AD=BC= ，则直线AB与CD所成角的余弦值为（ ）
    A.﹣
    B.﹣
    C.
    D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某市政府为了引导居民合理用水，决定全面实施阶梯水价，阶梯水价原则上以住宅（一套住宅为一户）的月用水量为基准定价：若用水量不超过12吨时，按4元/吨计算水费；若用水量超过12吨且不超过14吨时，超过12吨部分按6.60元/吨计算水费；若用水量超过14吨时，超过14吨部分按7.80元/吨计算水费．为了了解全市居民月用水量的分布情况，通过抽样，获得了100户居民的月用水量（单位：吨），将数据按照[0，2]，（2，4]，…，（14，16]分成8组，制成了如图1所示的频率分布直方图．
    （Ⅰ）假设用抽到的100户居民月用水量作为样本估计全市的居民用水情况．
    （ i）现从全市居民中依次随机抽取5户，求这5户居民恰好3户居民的月用水用量都超过12吨的概率；
    （ⅱ）试估计全市居民用水价格的期望（精确到0.01）；
    （Ⅱ）如图2是该市居民李某2016年1～6月份的月用水费y（元）与月份x的散点图，其拟合的线性回归方程是 ．若李某2016年1～7月份水费总支出为294.6元，试估计李某7月份的用水吨数．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知直三棱柱ABC﹣A1B1C1中，∠ABC=120°，AB=2，BC=CC1=1，则异面直线AB1与BC1所成角的余弦值为（ ）
    A.
    B.
    C.
    D.

    查看答案和解析>>

    同步练习册答案