
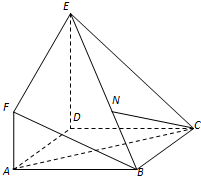
 如图,多面体EFABCD中,底面ABCD是正方形,AF⊥平面ABCD,DE∥AF,AB=DE=2,AF=1.
如图,多面体EFABCD中,底面ABCD是正方形,AF⊥平面ABCD,DE∥AF,AB=DE=2,AF=1.分析 (Ⅰ)法一:证明AC⊥平面BDE,即可证明BE⊥AC;
法二由已知得DE⊥平面ABCD,DA、DE、DC两两互相垂直,建立空间直角坐标系,利用向量法能证明BE⊥AC.
(Ⅱ)设$\overrightarrow{BN}=λ\overrightarrow{BE}(0≤λ≤1)$,$\overrightarrow{CN}=\overrightarrow{CB}+\overrightarrow{BN}=\overrightarrow{CB}+λ\overrightarrow{BE}$=(-2λ+2,-2λ,2λ),$\overrightarrow{CD}$为平面ADE的法向量,由此利用向量法能求出BN的长.
解答 (1)证明:法一:连结BD,∵ABCD是正方形,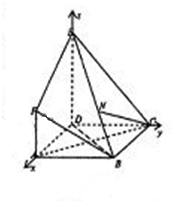
∴BD⊥AC.--------------------------------------(2分)
∵AF⊥平面ABCD,DE∥AF,
∴DE⊥平面ABCD,---------------------------(3分)
∴DE⊥AC,------------------------------(4分)
∵BD、DE在平面BDE内,且相交于D,
∴AC⊥平面BDE,-----------------------------(5分)
∴BE⊥AC.------------------------------------(6分)
法二:∵AF⊥平面ABCD,DE∥AF,∴DE⊥平面ABCD,又∵ABCD是正方形,∴DA、DE、DC两两互相垂直,可建立如图的空间直角坐标系,-(2分)
∴A(2,0,0),C(0,2,0),B(2,2,0),E(0,0,2),
∴$\overrightarrow{AC}=(-2,\;2,\;0)$,$\overrightarrow{BE}=(-2,-2,\;0)$,--------------------------------------------------------(4分)
∵$\overrightarrow{AC}•\overrightarrow{BE}=(-2)×(-2)+2×(-2)+0×0=0$,∴$\overrightarrow{AC}⊥\overrightarrow{BE}$,即BE⊥AC.-------------(6分)
(Ⅱ)解:∵AF⊥平面ABCD,DE∥AF,∴DE⊥平面ABCD,又∵ABCD是正方形,
∴DA、DE、DC两两互相垂直,可建立如图的空间直角坐标系,-------------------------(7分)
∴B(2,2,0),C(0,2,0),E(0,0,2),D(0,0,0),
∴$\overrightarrow{CB}=(2,\;0,\;0)$,$\overrightarrow{BE}=(-2,-2,\;2)$,$\overrightarrow{CD}=(0,-2,\;0)$,-----------------------------------(8分)
∵点N在棱BE上,∴可设$\overrightarrow{BN}=λ\overrightarrow{BE}(0≤λ≤1)$,
∴$\overrightarrow{CN}=\overrightarrow{CB}+\overrightarrow{BN}=\overrightarrow{CB}+λ\overrightarrow{BE}$=(-2λ+2,-2λ,2λ),------------------------------------(9分)
由于CD⊥平面ADE,∴$\overrightarrow{CD}$为平面ADE的法向量.------------------------------------(10分)
当直线CN与平面ADE成30°角时,$<\overrightarrow{CN},\overrightarrow{CD}>$=60°,
∴$cos<\overrightarrow{CN},\overrightarrow{CD}>=\frac{{\overrightarrow{CN}•\overrightarrow{CD}}}{{|{\overrightarrow{CN}}||{\overrightarrow{CD}}|}}=\frac{(-2λ+2,-2λ,\;2λ)•(0,-2,\;0)}{{\sqrt{{{(-2λ+2)}^2}+{{(-2λ)}^2}+{{(2λ)}^2}}×2}}=\frac{λ}{{\sqrt{3{λ^2}+2λ+1}}}$,$\frac{λ}{{\sqrt{3{λ^2}+2λ+1}}}=cos60°=\frac{1}{2}$,解得$λ=-1±\sqrt{2}$,∵0≤λ≤1,∴$λ=\sqrt{2}-1$,---(12分)
∴BN=|$\overrightarrow{BN}$|=λ|$\overrightarrow{BE}$|=($\sqrt{2}$-1)•$2\sqrt{3}$=2$\sqrt{6}$-2$\sqrt{3}$.------14
点评 本题主要考查空间线线垂直,线面垂直,直线与平面所成角,空间向量应用等基础知识;考查空间想象能力,运算求解能力,推理论证能力及探究能力.


 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①② | B. | ②③ | C. | ①③ | D. | ③④ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 年龄(岁) | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) | [65,75) |
| 频数 | 5 | 10 | 15 | 10 | 5 | 5 |
| 赞成人数 | 5 | 10 | 12 | 7 | 2 | 1 |
| 年龄不低于45岁的人 | 年龄低于45岁的人 | 合计 | |
| 赞成 | |||
| 不赞成 | |||
| 合计 |
| P(K2≥k0) | 0.050 | 0.010 | 0.001 |
| k0 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com