
分析 (1)通过当x≥3,当$-\frac{1}{2}≤x<3$,当$x<-\frac{1}{2}$时,化简函数f(x),利用函数f(x)>0分别求解解集即可.(2)令F(x)=f(x)+3|x-3|,利用绝对值三角不等式求解F(x)的最小值,然后求解t的取值范围.
解答 选修4-5:不等式选讲
解:(1)①当x≥3时,f(x)=2x+1-(x-3)=x+4>0,
得x>-4,所以x≥3成立;
②当$-\frac{1}{2}≤x<3$时,f(x)=2x+1+x-3=3x-2>0,
得$x>\frac{2}{3}$,所以$\frac{2}{3}<x<3$成立;
③当$x<-\frac{1}{2}$时,f(x)=-(2x+1)+x-3=-x-4>0,得x<-4,
所以x<-4成立.…(3分)
综上,原不等式的解集为$\left\{{x\left|{x<-4或x>\frac{2}{3}}\right.}\right\}$.…(5分)
(2)令F(x)=f(x)+3|x-3|=|2x+1|+2|x-3|≥|2x+1-(2x-6)|=7…(8分)
(当$-\frac{1}{2}≤x≤3$时等号成立).
所以t的取值范围为(-∞,7].…(10分)
点评 本题考查分类讨论思想的应用,绝对值不等式的解法,以及绝对值三角不等式的应用,考查转化思想以及计算能力.


 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
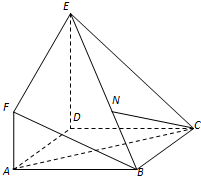 如图,多面体EFABCD中,底面ABCD是正方形,AF⊥平面ABCD,DE∥AF,AB=DE=2,AF=1.
如图,多面体EFABCD中,底面ABCD是正方形,AF⊥平面ABCD,DE∥AF,AB=DE=2,AF=1.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-5,5] | B. | [3,5] | C. | [3,4] | D. | [2,5] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 10个 | B. | 9个 | C. | 8个 | D. | 1个 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
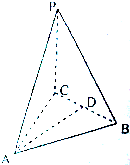 如图三棱锥P-ABC中,PC⊥平面ABC,PC=$\frac{2}{\sqrt{3}}$,D是BC的中点,且△ADC是边长为2的正三角形,求二面角P-AB-C的大小.
如图三棱锥P-ABC中,PC⊥平面ABC,PC=$\frac{2}{\sqrt{3}}$,D是BC的中点,且△ADC是边长为2的正三角形,求二面角P-AB-C的大小.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 点P是边长为2的正△ABC的边BC的中点,将△ACP沿AP折起,使得二面角C-AP-B为直二面角,点M为线段AC的中点,点N在线段BC上,且BN=2NC.
点P是边长为2的正△ABC的边BC的中点,将△ACP沿AP折起,使得二面角C-AP-B为直二面角,点M为线段AC的中点,点N在线段BC上,且BN=2NC.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com