
【题目】已知函数![]() .
.
(1)讨论![]() 在
在![]() 上的零点个数;
上的零点个数;
(2)当![]() 时,若存在
时,若存在![]() ,使
,使![]() ,求实数
,求实数![]() 的取值范围.(
的取值范围.(![]() 为自然对数的底数,其值为2.71828……)
为自然对数的底数,其值为2.71828……)
【答案】(1)见解析;(2)![]()
【解析】
(1)构造函数![]() ,先将讨论
,先将讨论![]() 在
在![]() 上的零点个数问题,转化为讨论直线
上的零点个数问题,转化为讨论直线![]() 与曲线
与曲线![]() 的交点个数问题,用导数方法研究函数
的交点个数问题,用导数方法研究函数![]() 单调性,求出值域,即可得出结果;
单调性,求出值域,即可得出结果;
(2)根据(1)的结果,由![]() 求出零点,得到
求出零点,得到![]() ,再由题意得到
,再由题意得到![]() 成立,构造函数
成立,构造函数![]() ,用导数方法研究其单调性,进而可求出结果.
,用导数方法研究其单调性,进而可求出结果.
(1)由![]() 得
得![]() ,令
,令![]() ,
,
因此讨论![]() 在
在![]() 上的零点个数,即是讨论直线
上的零点个数,即是讨论直线![]() 与曲线
与曲线![]() 的交点个数,
的交点个数,
∵![]() ,
,![]() 在
在![]() 上恒成立,
上恒成立,
故![]() 在
在![]() 上单调递增,
上单调递增,![]() ,
,
又![]() 连续不断,所以当
连续不断,所以当![]() 时,
时,![]() 在
在![]() 上无零点;
上无零点;
当![]() 时,
时,![]() 在
在![]() 上存在一个零点.
上存在一个零点.
(2)当![]() 时,由(1)得
时,由(1)得![]() 在
在![]() 上存在一个零点,
上存在一个零点,
由![]() 得
得![]() ,
,
由(1)可得![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增;
上单调递增;
所以![]() ,
,
又存在![]() ,使
,使![]() 成立,
成立,
所以,只需![]() 成立,即
成立,即![]() 不等式成立,
不等式成立,
令![]() ,
,
则![]() ,
,
易知![]() 在
在![]() 上恒成立,
上恒成立,
故![]() 在
在![]() 上单调递增
上单调递增
又![]() ,所以
,所以![]() .
.
故实数![]() 的取值范围为
的取值范围为![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】某公司想了解对某产品投入的宣传费用与该产品的营业额的影响.右图是以往公司对该产品的宣传费用![]() (单位:万元)和产品营业额
(单位:万元)和产品营业额![]() (单位:万元)的统计折线图.
(单位:万元)的统计折线图.

(Ⅰ)根据折线图可以判断,可用线性回归模型拟合宣传费用![]() 与产品营业额
与产品营业额![]() 的关系,请用相关系数加以说明;
的关系,请用相关系数加以说明;
(Ⅱ)建立产品营业额![]() 关于宣传费用
关于宣传费用![]() 的回归方程;
的回归方程;
(Ⅲ)若某段时间内产品利润![]() 与宣传费
与宣传费![]() 和营业额
和营业额![]() 的关系为
的关系为![]() 应投入宣传费多少万元才能使利润最大,并求最大利润. (计算结果保留两位小数)
应投入宣传费多少万元才能使利润最大,并求最大利润. (计算结果保留两位小数)
参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
参考公式:相关系数 ,回归方程
,回归方程![]() 中斜率和截距的最小二乘法估计公式分别为
中斜率和截距的最小二乘法估计公式分别为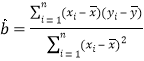 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】根据以往的经验,某建筑工程施工期间的降水量![]() (单位:
(单位:![]() )对工期的影响如下表:
)对工期的影响如下表:
降水量 |
|
|
|
|
工期延误天数 | 0 | 1 | 3 | 6 |
根据某气象站的资料,某调查小组抄录了该工程施工地某月前![]() 天的降水量的数据,绘制得到降水量的折线图,如下图所示.
天的降水量的数据,绘制得到降水量的折线图,如下图所示.

(1)求这![]() 天的平均降水量;
天的平均降水量;
(2)根据降水量的折线图,分别估计该工程施工延误天数![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某支教队有8名老师,现欲从中随机选出2名老师参加志愿活动,
(1)若规定选出的至少有一名女老师,则共有18种不同的需安排方案,试求该支教队男、女老师的人数;
(2)在(1)的条件下,记![]() 为选出的2位老师中女老师的人数,写出
为选出的2位老师中女老师的人数,写出![]() 的分布列.
的分布列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商品要了解年广告费![]() (单位:万元)对年利润
(单位:万元)对年利润![]() (单位:万元)的影响,对近4年的年广告费
(单位:万元)的影响,对近4年的年广告费![]() 和年利润
和年利润![]() 数据作了初步整理,得到下面的表格:
数据作了初步整理,得到下面的表格:
广告费 | 2 | 3 | 4 | 5 |
年利润 | 26 | 39 | 49 | 54 |
(Ⅰ)用广告费作解释变量,年利润作预报变量,建立![]() 关于
关于![]() 的回归直线方程;
的回归直线方程;
(Ⅱ)根据(Ⅰ)的结果预报广告费用为6万元时的年利润.
附:对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在正方体上任意选择![]() 个顶点,然后将它们两两相连,则可能组成的几何图形为_________(写出所有正确结论的编号).
个顶点,然后将它们两两相连,则可能组成的几何图形为_________(写出所有正确结论的编号).
①矩形;②不是矩形的平行四边形;③有三个面为等腰直角三角形,有一个面为等边三角形的四面体;④每个面都是等边三角形的四面体;⑤每个面都是直角三角形的四面体.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com