
【题目】已知函数![]() .
.
(1)当![]() 时,
时,![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(2)证明:当![]() 时,函数
时,函数![]() 有最小值,设
有最小值,设![]() 最小值为
最小值为![]() ,求函数
,求函数![]() 的值域.
的值域.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】分析:(1)原问题等价于![]() 对
对![]() 恒成立,设
恒成立,设![]() ,求其最小值即可;
,求其最小值即可;
(2)求导得 ,记
,记![]() ,
,![]() ,由(1)知
,由(1)知![]() 在区间
在区间![]() 内单调递增,从而得到当
内单调递增,从而得到当![]() 时,函数
时,函数![]() 有最小值;
有最小值; ,又因为
,又因为![]() .所以
.所以![]() ,从而易得函数
,从而易得函数![]() 的值域.
的值域.
详解:(1)因为![]() 对
对![]() 恒成立,
恒成立,
等价于![]() 对
对![]() 恒成立,设
恒成立,设![]() 得
得
![]() ,故
,故![]() 在
在![]() 上单调递增,
上单调递增,
当![]() 时,由上知
时,由上知![]() ,所以
,所以![]() ,即
,即![]() ,
,
所以实数![]() 的取值范围为
的取值范围为![]() ;
;
(2)对![]() 求导得
求导得 ,
,
记![]() ,
,![]() ,
,
由(1)知![]() 在区间
在区间![]() 内单调递增,又
内单调递增,又![]() ,
,
所以存在唯一正实数![]() ,使得
,使得![]() ,
,
![]() 当
当![]() 时,
时,![]() ,
,![]() ,函数
,函数![]() 在区间
在区间![]() 单调递减;
单调递减;
![]() 时,
时,![]() ,
,![]() ,函数
,函数![]() 在区间
在区间![]() 单调递增;
单调递增;
所以![]() 在
在![]() 内有最小值
内有最小值 ,
,
由题设即 .
.
又因为![]() .所以
.所以![]() .
.
根据(1)知, ![]() 在
在![]() 内单调递增,
内单调递增,![]() ,
,
所以![]() .令
.令![]() ,则
,则
![]() ,函数
,函数![]() 在区间
在区间![]() 内单调递增,
内单调递增,
所以![]() ,
,
即函数![]() 的值域为
的值域为![]() .
.


科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在极坐标系中,曲线![]() ,
,![]() ,C与l有且仅有一个公共点.
,C与l有且仅有一个公共点.
(Ⅰ)求a;
(Ⅱ)O为极点,A,B为C上的两点,且![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在正方形![]() 中,
中,![]() 是
是![]() 的中点,点
的中点,点![]() 在线段
在线段![]() 上,且
上,且![]() .若将
.若将![]() 分别沿
分别沿![]() 折起,使
折起,使![]() 两点重合于点
两点重合于点![]() ,如图2.
,如图2.
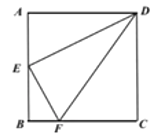
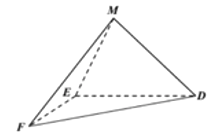
图1 图2
(1)求证:![]() 平面
平面![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)对任意x,y∈R,总有f(x)+f(y)=f(x+y),且当x>0时,f(x)<0,f(1)=-![]() .
.
(1)求证:f(x)是R上的单调减函数.
(2)求f(x)在[-3,3]上的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】轮船A从某港口O要将一些物品送到正航行的轮船B上,在轮船A出发时,轮船B位于港口O北偏西30°且与O相距20海里的P处,并正以15海里/时的航速沿正东方向匀速行驶,假设轮船A沿直线方向以v海里/时的航速匀速行驶,经过t小时与轮船B相遇,
(1)若使相遇时轮船A航距最短,则轮船A的航行速度的大小应为多少?
(2)假设轮船B的航行速度为30海里/时,轮船A的最高航速只能达到30海里/时,则轮船A以多大速度及沿什么航行方向行驶才能在最短时间内与轮船B相遇,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)是R上的奇函数,且x>0时,f(x)=x2-4x+3.
求:(1)f(x)的解析式.
(2)已知t>0,求函数f(x)在区间[t,t+1]上的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在矩形ABCD和矩形ABEF中,![]() ,
,![]() ,矩形ABEF可沿AB任意翻折.
,矩形ABEF可沿AB任意翻折.
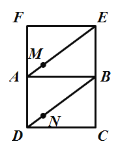
(1)求证:当点F,A,D不共线时,线段MN总平行于平面ADF.
(2)“不管怎样翻折矩形ABEF,线段MN总与线段FD平行”这个结论正确吗?如果正确,请证明;如果不正确,请说明能否改变个别已知条件使上述结论成立,并给出理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com