Question

3．如图所示，在正方体ABCD-A₁B₁C₁D₁中，点M在B₁C上，点N在BD上，并且MN∥平面AA₁B₁B，求证：CM=DN．

Answer 1

分析 过M作MM₁⊥BB₁，过N作NN₁⊥AB，由于MN‖平面AA₁B₁B，可得MM₁=NN₁，通过证明三角形B₁MM₁和三角形BNN₁全等，从而可证B₁M=BN，结合B₁C=BD，即可证明故CM=DN．

解答 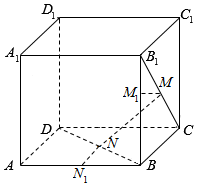证明：过M作MM₁⊥BB₁，过N作NN₁⊥AB，
易证得MM₁⊥面ABB₁A₁，NN₁⊥面ABB₁A₁，
故MM₁为M到面ABB₁A₁的距离，NN₁为N到面ABB₁A₁的距离，
又由于MN‖平面AA₁B₁B，
所以可知MM₁=NN₁，
三角形B₁MM₁和三角形BNN₁都是直角三角形，∠ABD=∠BB₁C=45°，MM₁=NN₁，
故两三角形全等，
从而B₁M=BN，
而B₁C=BD，
故CM=DN．

点评 本题主要考查了线面平行的性质，三角形全等的判定和性质，考查了空间想象能力和推理论证能力，属于中档题．