
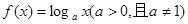 在(0,+∞)上单调递增,则f (a+1)与f (2)的大小关系是
在(0,+∞)上单调递增,则f (a+1)与f (2)的大小关系是| A.f (a+1)= f (2) | B.f (a+1)> f (2) |
| C.f (a+1)< f (2) | D.不确定 |
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
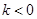 ,函数
,函数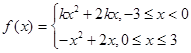
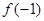 ,
,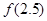 的值;
的值;  在
在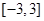 上的单调性;
上的单调性; 在
在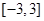 上的最小值与最大值,并求出相应的自变量的取值.
上的最小值与最大值,并求出相应的自变量的取值.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
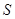 平方米.
平方米.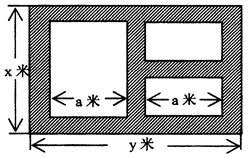
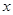 表示
表示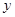 和用
和用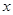 表示
表示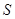 的函数关系式(写出函数定义域);
的函数关系式(写出函数定义域);查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
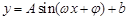 的图像.2013年1月下旬荆门地区连续几天最高温度都出现在14时,最高温度为
的图像.2013年1月下旬荆门地区连续几天最高温度都出现在14时,最高温度为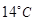 ;最低温度出现在凌晨2时,最低温度为零下
;最低温度出现在凌晨2时,最低温度为零下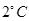 .
.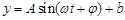
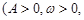
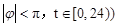 的表达式;
的表达式;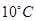 ,教室就要开空调,请问届时学校后勤应该送电吗?
,教室就要开空调,请问届时学校后勤应该送电吗?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com