练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

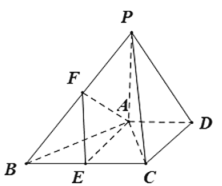
    【题目】如图，已知四棱锥中，底面为直角梯形，，，，平面，，分别是，的中点.

    （1）证明：；

    （2）若，求点到平面的距离.

    【答案】(1)证明见详解；(2)

    【解析】

    （1）先证明直线AE垂直于平面PAD，再由线面垂直证明线线垂直；

    （2）根据等体积法，将问题转化为求解三棱锥的体积即可.

    （1）因为E为BC中点，且，故AD=EC，又AD//EC，

    故四边形AECD为平行四边形，故AE//CD，又CD，

    故AEAD；

    因为PA底面ABCD，AE平面ABCD，故PAAE

    又AD平面PAD，PA平面PAD，

    故AE平面PAD，又PD平面PAD

    故AEPD.即证.

    （2）在中，AF为斜边上的中线，又因为PA=AB=2，且PAAB

    故可得：AF=；

    在中，因为AB=2，BE=1，且AEBE，故可得AE=

    故可得

    在中，因为PA=2=AC，且PA，故可得PC=

    在中，因为EF分别为两边的中点，故EF=

    故由余弦定理可得，则.

    故.

    又因为F为PB的中点，且PA平面ABCD，

    故F点到平面ABCD的距离为

    设点C到平面AEF的距离为，

    根据，即

    解得.

    故点到平面的距离为.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】某民航部门统计的2019年春运期间12个城市售出的往返机票的平均价格以及相比上年同期变化幅度的数据统计图表如图所示，根据图表，下面叙述不正确的是( )

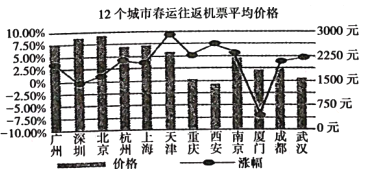
    A. 同去年相比，深圳的变化幅度最小且厦门的平均价格有所上升

    B. 天津的平均价格同去年相比涨幅最大且2019年北京的平均价格最高

    C. 2019年平均价格从高到低居于前三位的城市为北京、深圳、广州

    D. 同去年相比，平均价格的涨幅从高到低居于前三位的城市为天津、西安、南京

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆经过点，离心率为，过点的直线与椭圆交于不同的两点，

    （1）求椭圆的方程；

    （2）求的取值范围；

    （3）设直线和的斜率分别为和，求证:为定值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数．

    （1）当时，求函数在上的最小值；

    （2）若，求证：．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在△ABC中，内角A,B,C所对的边分别为a,b,c．已知a＝2,c＝3，又知bsinA＝acos（B）．

    （Ⅰ）求角B的大小、b边的长：

    （Ⅱ）求sin（2A﹣B）的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】经过多年的努力，炎陵黄桃在国内乃至国际上逐渐打开了销路，成为炎陵部分农民脱贫致富的好产品.为了更好地销售，现从某村的黄桃树上随机摘下了100个黄桃进行测重，其质量分布在区间内（单位：克），统计质量的数据作出其频率分布直方图如图所示：

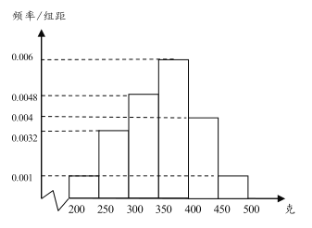
    （1）按分层抽样的方法从质量落在，的黄桃中随机抽取5个，再从这5个黄桃中随机抽2个，求这2个黄桃质量至少有一个不小于400克的概率；

    （2）以各组数据的中间数值代表这组数据的平均水平，以频率代表概率，已知该村的黄桃树上大约还有100000个黄桃待出售，某电商提出两种收购方案：

    A.所有黄桃均以20元/千克收购；

    B.低于350克的黄桃以5元/个收购，高于或等于350克的以9元/个收购.

    请你通过计算为该村选择收益最好的方案.

    （参考数据：）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某水果种植基地引进一种新水果品种，经研究发现该水果每株的产量（单位：）和与它“相近”的株数具有线性相关关系（两株作物“相近”是指它们的直线距离不超过），并分别记录了相近株数为0，1，2，3，4时每株产量的相关数据如下：

    0

    1

    2

    3

    4

    15

    12

    11

    9

    8

    （1）求出该种水果每株的产量关于它“相近”株数的回归方程；

    （2）有一种植户准备种植该种水果500株，且每株与它“相近”的株数都为，计划收获后能全部售出，价格为10元，如果收入（收入=产量×价格）不低于25000元，则的最大值是多少？

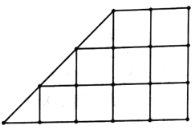
    （3）该种植基地在如图所示的直角梯形地块的每个交叉点（直线的交点）处都种了一株该种水果，其中每个小正方形的边长和直角三角形的直角边长都为，已知该梯形地块周边无其他树木影响，若从所种的该水果中随机选取一株，试根据（1）中的回归方程，预测它的产量的分布列与数学期望.

    附：回归方程中斜率和截距的最小二乘法估计公式分别为：，.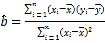

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，为自然对数的底数.

    （1）当时，证明，，；

    （2）若函数在上存在极值点，求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

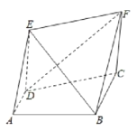
    【题目】如图所示,直角梯形中,,,,四边形为矩形,.

    （1）求证:平面平面;

    （2）在线段上是否存在点,使得直线与平面所成角的正弦值为,若存在,求出线段的长,若不存在,请说明理由.

    查看答案和解析>>

    同步练习册答案