
用0,1,2,3,4,5这六个数字:
(1)能组成多少个无重复数字的四位偶数?
(2)能组成多少个无重复数字且为5的倍数的五位数?
(3)能组成多少个无重复数字且比1325大的四位数?
(1)符合要求的四位偶数可分为三类:
第一类:0在个位时有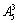 个;
个;
第二类:2在个位时,首位从1,3,4,5中选定1个(有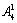 种),十位和百位从余下的数字中选(有
种),十位和百位从余下的数字中选(有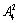 种),于是有
种),于是有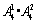 个;
个;
第三类:4在个位时,与第二类同理,也有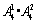 个.
个.
由分类加法计数原理知,共有四位偶数: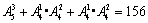 个.
个.
(2)符合要求的五位数中5的倍数的数可分为两类:个位数上的数字是0的五位数有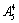 个;个位数上的数字是5的五位数有
个;个位数上的数字是5的五位数有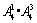 个.故满足条件的五位数的个数共有
个.故满足条件的五位数的个数共有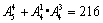 个.
个.
(3)符合要求的比1325大的四位数可分为三类:
第一类:形如2□□□,3□□□,4□□□,5□□□,共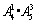 个;
个;
第二类:形如14□□,15□□,共有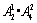 个;
个;
第三类:形如134□,135□,共有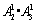 个;
个;
由分类加法计数原理知,无重复数字且比1325大的四位数共有:
 个.
个.


科目:高中数学 来源: 题型:
中、印两国争夺某项国际博览会的申办权,进入最后一道程序,由国际展览局三名执委投票,决定承办权的最后归属。资料显示,A,B,C三名执委投票意向如下表所示
|
| 中 国 | 印度 |
| A |
|
|
| B |
|
|
| C |
|
|
规定每位执委只有一票,且不能弃权,已知中国获得两票的概率为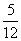 。
。
(1)求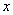 ,
,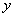 的值;
的值;
(2)设中国获得的票数为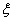 ,试写出
,试写出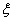 的概率分布列,并求E
的概率分布列,并求E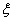 。
。
查看答案和解析>>
科目:高中数学 来源: 题型:
假设洗小水壶需一分钟,烧开水需15分钟,洗茶杯需3分钟,取放茶叶需2分钟,泡茶需1分钟则上述“喝茶问题”中至少需多少分钟才可以喝上茶? ( )
A . 16 B. 17 C. 18 D. 19
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com