
【题目】已知函数f(x)![]() 是定义在(﹣1,1)上的奇函数,且f(
是定义在(﹣1,1)上的奇函数,且f(![]() )
)![]() .
.
(Ⅰ)求实数m,n的值,并用定义证明f(x)在(﹣1,1)上是增函数;
(Ⅱ)设函数g(x)是定义在(﹣1,1)上的偶函数,当x∈[0,1)时,g(x)=f(x),求函数g(x)的解析式.
【答案】(Ⅰ)m=1,n=0,见解析;(Ⅱ)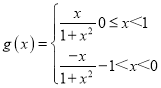
【解析】
(Ⅰ)根据奇函数的性质,f(0)=0,求得n,再根据f(![]() )
)![]() ,求得m,再结合增减函数的定义证明即可;
,求得m,再结合增减函数的定义证明即可;
(II)可设﹣1<x<0,则0<﹣x<1,将![]() 代入x∈[0,1)时对应的表达式,再结合偶函数定义即可求解;
代入x∈[0,1)时对应的表达式,再结合偶函数定义即可求解;
(Ⅰ)因为f(x)![]() 是定义在(﹣1,1)上的奇函数,所以f(0)=0,即n=0,
是定义在(﹣1,1)上的奇函数,所以f(0)=0,即n=0,
又因为f(![]() )
)![]() ,所以
,所以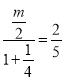 ,解得m=1,所以m=1,n=0,经检验成立;
,解得m=1,所以m=1,n=0,经检验成立;
因为﹣1<x1<x2<1,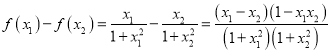 ,
,
因为﹣1<x1<x2<1,所以x1﹣x2<0,1﹣x1x2>0,所以f(x1)<f(x2)
所以f(x)在(﹣1,1)上是增函数;
(Ⅱ)因为函数g(x)是定义在(﹣1,1)上的偶函数,且当x∈[0,1)时,g(x)=f(x)![]() ,
,
令﹣1<x<0,则0<﹣x<1,g(﹣x)![]() g(x),
g(x),
所以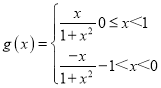 .
.


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,
为参数,![]() ),已知直线
),已知直线![]() 的方程为
的方程为![]() .
.
(1)设![]() 是曲线
是曲线![]() 上的一个动点,当
上的一个动点,当![]() 时,求点
时,求点![]() 到直线
到直线![]() 的距离的最小值;
的距离的最小值;
(2)若曲线![]() 上的所有点均在直线
上的所有点均在直线![]() 的右下方,求
的右下方,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场举行有奖促销活动,顾客购买一定金额的商品后即可抽奖.每次抽奖都是从装有4个红球、6个白球的甲箱和装有5个红球、5个白球的乙箱中,各随机摸出1个球,在摸出的2个球中,若都是红球,则获一等奖;若只有1个红球,则获二等奖;若没有红球,则不获奖.
(1)求顾客抽奖1次能获奖的概率;
(2)若某顾客有3次抽奖机会,记该顾客在3次抽奖中获一等奖的次数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直四棱柱![]() 中,底面
中,底面![]() 为等腰梯形,
为等腰梯形,![]() .
.

(1)证明:![]() ;
;
(2)设![]() 是线段
是线段![]() 上的动点,是否存在这样的点
上的动点,是否存在这样的点![]() ,使得二面角
,使得二面角![]() 的余弦值为
的余弦值为![]() ,如果存在,求出
,如果存在,求出![]() 的长;如果不存在,请说明理由.
的长;如果不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某同学解答一道解析几何题:“已知直线l:![]() 与x轴的交点为A,圆O:
与x轴的交点为A,圆O:![]() 经过点A.
经过点A.
(Ⅰ)求r的值;
(Ⅱ)若点B为圆O上一点,且直线AB垂直于直线l,求![]() .”
.”
该同学解答过程如下:
解答:(Ⅰ)令![]() ,即
,即![]() ,解得
,解得![]() ,所以点A的坐标为
,所以点A的坐标为![]() .
.
因为圆O:![]() 经过点A,所以
经过点A,所以![]() .
.
(Ⅱ)因为![]() .所以直线AB的斜率为
.所以直线AB的斜率为![]() .
.
所以直线AB的方程为![]() ,即
,即![]() .
.
代入![]() 消去y整理得
消去y整理得![]() ,
,
解得![]() ,
,![]() .当
.当![]() 时,
时,![]() .所以点B的坐标为
.所以点B的坐标为![]() .
.
所以 .
.
指出上述解答过程中的错误之处,并写出正确的解答过程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】土壤重金属污染已经成为快速工业化和经济高速增长地区的一个严重问题,污染土壤中的某些重金属易被农作物吸收,并转入食物链影响大众健康.A,B两种重金属作为潜在的致癌物质,应引起特别关注.某中学科技小组对由A,B两种重金属组成的1000克混合物进行研究,测得其体积为100立方厘米(不考虑物理及化学变化),已知重金属A的密度大于![]() ,小于
,小于![]() ,重金属B的密度为
,重金属B的密度为![]() .试计算此混合物中重金属A的克数的范围.
.试计算此混合物中重金属A的克数的范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】小明在10场篮球比赛中的投篮情况统计如下(假设各场比赛相互独立):
场次 | 投篮次数 | 命中次数 |
主场1 | 22 | 12 |
主场2 | 15 | 12 |
主场3 | 12 | 8 |
主场4 | 23 | 8 |
主场5 | 24 | 20 |
场次 | 投篮次数 | 命中次数 |
客场1 | 18 | 8 |
客场2 | 13 | 12 |
客场3 | 21 | 7 |
客场4 | 18 | 15 |
客场5 | 25 | 12 |
(1)从上述比赛中随机选择一场,求小明在该场比赛中投篮命中率超过0.6的概率;
(2)从上述比赛中随机选择一个主场和一个客场,求小明的投篮命中率一场超过0.6,一场不超过0.6的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为研究某种图书每册的成本费![]() (元)与印刷数
(元)与印刷数![]() (千册)的关系,收集了一些数据并作了初步处理,得到了下面的散点图及一些统计量的值.
(千册)的关系,收集了一些数据并作了初步处理,得到了下面的散点图及一些统计量的值.

|
|
|
|
|
|
|
15.25 | 3.63 | 0.269 | 2085.5 |
| 0.787 | 7.049 |
表中![]() ,
, ![]() .
.
(1)根据散点图判断: ![]() 与
与![]() 哪一个更适宜作为每册成本费
哪一个更适宜作为每册成本费![]() (元)与印刷数
(元)与印刷数![]() (千册)的回归方程类型?(只要求给出判断,不必说明理由)
(千册)的回归方程类型?(只要求给出判断,不必说明理由)
(2)根据(1)的判断结果及表中数据,建立![]() 关于
关于![]() 的回归方程(回归系数的结果精确到0.01);
的回归方程(回归系数的结果精确到0.01);
(3)若每册书定价为10元,则至少应该印刷多少册才能使销售利润不低于78840元?(假设能够全部售出,结果精确到1)
(附:对于一组数据![]() ,
, ![]() ,…,
,…, ![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为 ,
, ![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com