选修4-5:不等式选讲
已知函数f(x)=|x+1|+|x-2|-m
(I)当m=5时,求f(x)>0的解集;
(II)若关于x的不等式f(x)≥2的解集是R,求m的取值范围.
解:(I)当m=5时,原不等式可化为:|x+1|+|x-2|>5,
①
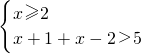
,解之,得x>3;
②
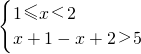
,解之,得不存在符合题意的实数x;
③
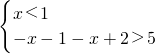
,解之,得x<-2
综上所述,当m=5时,f(x)>0的解集为(-∞,-2)∪(3,+∞) …(5分)
(II)不等式f(x)≥2即|x+1|+|x-2|>m+2,
∵x∈R时,恒有|x+1|+|x-2|≥|(x+1)-(x-2)|=3,
∴要使不等式|x+1|+|x-2|≥m+2 解集是R,必定有m+2≤3,即m≤1
由此可得:m的取值范围是(-∞,1). …(10分)
分析:(I)当m=5时,原不等式可化为|x+1|+|x-2|>5,分三种情况去绝对值,对不等式加以讨论,最后综合即得到f(x)>0的解集;
(II)关于x的不等式f(x)≥2的解集是R,根据绝对值不等式的性质,可得|x+1|+|x-2|的最小值3大于或等于m+2,由此可得实数m的取值范围.
点评:本题给出含有绝对值的函数,讨论不等式f(x)>m(m是常数)的解集的问题,着重考查了绝对值的定义与性质和不等式恒成立问题的处理方法等知识,属于基础题.

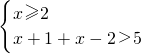 ,解之,得x>3;
,解之,得x>3;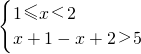 ,解之,得不存在符合题意的实数x;
,解之,得不存在符合题意的实数x;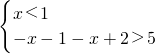 ,解之,得x<-2
,解之,得x<-2
