
【题目】已知函数f(x)=xlnx的图象上有A、B两点,其横坐标为x1 , x2(0<x1<x2<1)且满足f(x1)=f(x2),若k=5( ![]() +
+ ![]() ),且k为整数时,则k的值为( )(参考数据:e≈2.72)
),且k为整数时,则k的值为( )(参考数据:e≈2.72)
A.1
B.2
C.3
D.4
【答案】C
【解析】解:∵f(x)=xlnx,∴f′(x)=1+lnx,x>0, 由f′(x)=0,得x= ![]() ,
,
∵函数f(x)=xlnx的图象上有A、B两点,其横坐标为x1 , x2(0<x1<x2<1)且满足f(x1)=f(x2),
∴x1lnx1=x2lnx2 ,
(0<x1< ![]() <x2<1),如图所示,
<x2<1),如图所示,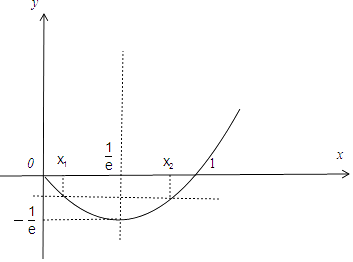
由 ![]() ,
, ![]() ,
,![]() <
< ![]() +
+ ![]() =
= ![]() ,
,
∵t= ![]() 关于x1单调递减,0<x1<
关于x1单调递减,0<x1< ![]() ,
,
∴ ![]() <
< ![]() ,∴5(
,∴5( ![]() +
+ ![]() )<
)< ![]() ,
,
∴k≤3.
∴k为整数时,则k的值为3.
故选:C.
【考点精析】本题主要考查了函数的极值与导数的相关知识点,需要掌握求函数![]() 的极值的方法是:(1)如果在
的极值的方法是:(1)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极大值(2)如果在
是极大值(2)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极小值才能正确解答此题.
是极小值才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】已知两圆x2+y2﹣2x+10y﹣24=0和 x2+y2+2x+2y﹣8=0
(1)判断两圆的位置关系;(2)求公共弦所在的直线方程及公共弦的长
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知直线l过定点P(1,1),且倾斜角为 ![]() ,以坐标原点为极点,x轴的正半轴为极轴的坐标系中,曲线C的极坐标方程为
,以坐标原点为极点,x轴的正半轴为极轴的坐标系中,曲线C的极坐标方程为 ![]() .
.
(1)求曲线C的直角坐标方程与直线l的参数方程;
(2)若直线l与曲线C相交于不同的两点A,B,求|AB|及|PA||PB|的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示的是自动通风设施![]() 该设施的下部ABCD是等腰梯形,其中
该设施的下部ABCD是等腰梯形,其中![]() 米,高
米,高![]() 米,
米,![]() 米
米![]() 上部CmD是个半圆,固定点E为CD的中点
上部CmD是个半圆,固定点E为CD的中点![]() 是由电脑控制其形状变化的三角通风窗
是由电脑控制其形状变化的三角通风窗![]() 阴影部分均不通风
阴影部分均不通风![]() ,MN是可以沿设施边框上下滑动且始终保持和CD平行的伸缩横杆.
,MN是可以沿设施边框上下滑动且始终保持和CD平行的伸缩横杆.
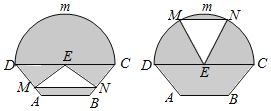
![]() 设MN与AB之间的距离为x米,试将三角通风窗
设MN与AB之间的距离为x米,试将三角通风窗![]() 的通风面积
的通风面积![]() 平方米
平方米![]() 表示成关于x的函数
表示成关于x的函数![]() ;
;
![]() 当MN与AB之间的距离为多少米时,三角通风窗
当MN与AB之间的距离为多少米时,三角通风窗![]() 的通风面积最大?求出这个最大面积.
的通风面积最大?求出这个最大面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】△ABC中,内角A,B,C的对边分别为a,b,c,且cos2A=3cos(B+C)+1.
(Ⅰ)求角A的大小;
(Ⅱ)若cosBcosC=﹣ ![]() ,且△ABC的面积为2
,且△ABC的面积为2 ![]() ,求a.
,求a.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,将边长为2的正方体![]() 沿对角线
沿对角线![]() 折起,得到三棱锥
折起,得到三棱锥![]() ,则下列命题中,错误的为( )
,则下列命题中,错误的为( )
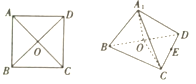
A. 直线![]() 平面
平面![]()
B. ![]()
C. 三棱锥![]() 的外接球的半径为
的外接球的半径为![]()
D. 若![]() 为
为![]() 的中点,则
的中点,则![]() 平面
平面![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() (
(![]() )的右焦点为
)的右焦点为![]() ,右顶点为
,右顶点为![]() ,已知
,已知![]() ,其中
,其中![]() 为原点,
为原点,![]() 为椭圆的离心率.
为椭圆的离心率.
(Ⅰ)求椭圆的方程;
(Ⅱ)设过点![]() 的直线
的直线![]() 与椭圆交于点
与椭圆交于点![]() (
(![]() 不在
不在![]() 轴上),垂直于
轴上),垂直于![]() 的直线与
的直线与![]() 交于点
交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,若
,若![]() ,且
,且![]() ,求直线的
,求直线的![]() 斜率.
斜率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com