
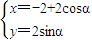 (α为参数),若以点O(0,0)为极点,x正半轴为极轴建立极坐标系,则该曲线的极坐标方程是 .
(α为参数),若以点O(0,0)为极点,x正半轴为极轴建立极坐标系,则该曲线的极坐标方程是 .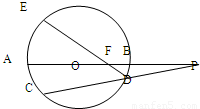
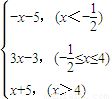 ,
, 时,f(x)>2?-x-5>2,
时,f(x)>2?-x-5>2, ≤x≤4时,f(x)>2?3x-3>2,
≤x≤4时,f(x)>2?3x-3>2, <x≤4;
<x≤4; };
}; 得其普通方程为:(x+2)2+y2=4,
得其普通方程为:(x+2)2+y2=4,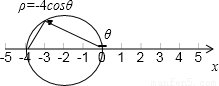

 弧EC的度数=弧AC的度数
弧EC的度数=弧AC的度数 =
=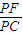 ,
,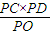 =
= =2×
=2× =3.
=3. };B,ρ=-4cosθ;C,3.
};B,ρ=-4cosθ;C,3.

 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:高中数学 来源: 题型:
 (考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评分)
(考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评分)
|
查看答案和解析>>
科目:高中数学 来源: 题型:
 (三选一,考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评分)
(三选一,考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评分)
|
| 3 |
| 3 |
| 5 |
| 3 |
| 5 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评阅记分)
(考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评阅记分)| π |
| 4 |
| 2 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评阅记分)
(考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评阅记分)
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
|
| 4 |
| a |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com