
分析 由题意,画出图形,利用定积分的几何意义表示围成部分的面积求值.
解答  解:由曲线y=-x2+2x与y=1-$\sqrt{1-{x}^{2}}$所围成的图形如图阴影部分:
解:由曲线y=-x2+2x与y=1-$\sqrt{1-{x}^{2}}$所围成的图形如图阴影部分:
其面积为$\frac{1}{4}π×{1}^{2}-{∫}_{0}^{1}(1+{x}^{2}-2x)dx$=$\frac{π}{4}-(x+\frac{1}{3}{x}^{3}-{x}^{2}){|}_{0}^{1}$=$\frac{π}{4}-\frac{1}{3}$;
故答案为:$\frac{π}{4}-\frac{1}{3}$.
点评 本题考查了定积分的几何意义;关键是正确利用定积分表示封闭图形的面积.


 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 单价x | 80 | 82 | 84 | 86 | 88 | 90 |
| 销量y | 90 | 84 | 83 | 80 | 75 | 68 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 假设n=k(k∈N*)时命题成立 | B. | 假设n≥k(k∈N*)时命题成立 | ||
| C. | 假设n=2k(k∈N*)时命题成立 | D. | 假设n=2(k+1)(k∈N*)时命题成立 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
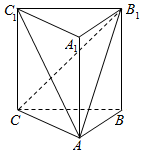 如图,直三棱柱ABC-A1B1C1中,底面是∠A=90°的直角三角形,且AB=1,BB1=2,直线B1C与平面ABC成30°角.
如图,直三棱柱ABC-A1B1C1中,底面是∠A=90°的直角三角形,且AB=1,BB1=2,直线B1C与平面ABC成30°角.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
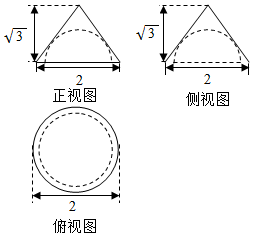 已知一个几何体的三视图如图所示,则该几何体表面积为( )
已知一个几何体的三视图如图所示,则该几何体表面积为( )| A. | 3π | B. | $\frac{15π}{4}$ | C. | $\frac{3\sqrt{3}π}{4}$ | D. | 6π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com