
【题目】已知![]() ,
, ![]() 为实数,函数
为实数,函数![]() ,函数
,函数![]() .
.
(1) 当![]() 时,令
时,令![]() ,若
,若![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(2) 当![]() 时,令
时,令![]() ,是否存在实数
,是否存在实数![]() ,使得对于函数
,使得对于函数![]() 定义域中的任意实数
定义域中的任意实数![]() ,均存在实数
,均存在实数![]() ,有
,有![]() 成立?若存在,求出实数
成立?若存在,求出实数![]() 的取值集合;若不存在,请说明理由.
的取值集合;若不存在,请说明理由.
【答案】(1)![]() ;(2)见解析
;(2)见解析
【解析】试题分析:(1)![]() 恒成立,等价于
恒成立,等价于![]() 恒成立,利用导数研究函数的单调性,求出
恒成立,利用导数研究函数的单调性,求出![]() 的最大值即可得结果;(2)
的最大值即可得结果;(2) ![]() 时,
时, ![]()
![]() ,对
,对![]() 分两种情况讨论,分别利用导数研究函数的单调性(需要两次求导),利用单调性结合函数图象,排除不合题意的
分两种情况讨论,分别利用导数研究函数的单调性(需要两次求导),利用单调性结合函数图象,排除不合题意的![]() 值进而可得
值进而可得
试题解析:(1) 当![]() 时,
时, ![]()
![]() 在
在![]() 上递增,在
上递增,在![]() 上递减,可得
上递减,可得![]() 的最大值为
的最大值为![]() ,所以可得)
,所以可得)![]() .
.
(2) 当a=-1时,假设存在实数b满足条件,则G(x)=![]() lnx≥1在x∈(0,1)∪(1,+∞)上恒成立.
lnx≥1在x∈(0,1)∪(1,+∞)上恒成立.
1) 当x∈(0,1)时,G(x)=![]() lnx≥1可化为(bx+1-b)lnx-x+1≤0,
lnx≥1可化为(bx+1-b)lnx-x+1≤0,
令H(x)=(bx+1-b)lnx-x+1,x∈(0,1),
问题转化为:H(x)≤0对任意x∈(0,1)恒成立(*);
则H(1)=0,H′(x)=blnx+![]() +b-1,H′(1)=0.
+b-1,H′(1)=0.
令Q(x)=blnx+![]() +b-1,则Q′(x)=
+b-1,则Q′(x)=![]() .
.
① b≤![]() 时,因为b(x+1)-1≤
时,因为b(x+1)-1≤![]() (x+1)-1<
(x+1)-1<![]() ×2-1=0,
×2-1=0,
故Q′(x)<0,所以函数y=Q(x)在x∈(0,1)时单调递减,Q(x)>Q(1)=0,
即H′(x)>0,从而函数y=H(x)在x∈(0,1)时单调递增,
故H(x)<H(1)=0,所以(*)成立,满足题意;
② 当b>![]() ,Q′(x)=
,Q′(x)=![]() =
= ,
,
因为b>![]() ,所以
,所以![]() -1<1,记I=
-1<1,记I=![]() ∩(0,1),则当x∈I时,x-
∩(0,1),则当x∈I时,x-![]() >0,
>0,
故Q′(x)>0,所以函数y=Q(x)在x∈I时单调递增,Q(x)<Q(1)=0,
即H′(x)<0,从而函数y=H(x)在x∈I时单调递减,所以H(x)>H(1)=0,此时(*)不成立;
所以当x∈(0,1),G(x)=![]() lnx≥1恒成立时,b≤
lnx≥1恒成立时,b≤![]() ;
;
2) 当x∈(1,+∞)时,G(x)=![]() lnx≥1可化为(bx+1-b)lnx-x+1≥0,
lnx≥1可化为(bx+1-b)lnx-x+1≥0,
令H(x)=(bx+1-b)lnx-x+1,x∈(1,+∞),问题转化为:
H(x)≥0对任意的x∈(1,+∞)恒成立(**);则H(1)=0,H′(x)=blnx+![]() +b-1,H′(1)=0.
+b-1,H′(1)=0.
令Q(x)=blnx+![]() +b-1,则Q′(x)=
+b-1,则Q′(x)=![]() .
.
① b≥![]() 时,b(x+1)-1>2b-1≥
时,b(x+1)-1>2b-1≥![]() ×2-1=0,
×2-1=0,
故 Q′(x)>0,所以函数y=Q(x)在x∈(1,+∞)时单调递增,Q(x)>Q(1)=0,即H′(x)>0,
从而函数y=H(x)在x∈(1,+∞)时单调递增,所以H(x)>H(1)=0,此时(**)成立;
② 当b<![]() 时,
时,
ⅰ) 若 b≤0,必有Q′(x)<0,故函数y=Q(x)在x∈(1,+∞)上单调递减,
所以Q(x)<Q(1)=0,即H′(x)<0,
从而函数y=H(x)在x∈(1,+∞)时单调递减,所以H(x)<H(1)=0,此时(**)不成立;
ⅱ) 若0<b<![]() ,则
,则![]() -1>1,所以x∈
-1>1,所以x∈![]() 时,Q′(x)=
时,Q′(x)=![]() =
= <0,
<0,
故函数y=Q(x)在x∈![]() 上单调递减,Q(x)<Q(1)=0,即H′(x)<0,
上单调递减,Q(x)<Q(1)=0,即H′(x)<0,
所以函数y=H(x)在x∈![]() 时单调递减,所以H(x)<H(1)=0,此时(**)不成立;
时单调递减,所以H(x)<H(1)=0,此时(**)不成立;
所以当x∈(1,+∞),G(x)=![]() lnx≥1恒成立时,b≥
lnx≥1恒成立时,b≥![]() .(15分)
.(15分)
综上所述,当x∈(0,1)∪(1,+∞),G(x)=![]() lnx≥1恒成立时,b=
lnx≥1恒成立时,b=![]() ,从而实数b的取值集合为
,从而实数b的取值集合为![]() .
.


 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:高中数学 来源: 题型:
【题目】如图,直三棱柱![]() 中,
中,![]() ,
,![]() ,
,![]() 是
是![]() 的中点,
的中点,![]() 是等腰三角形,
是等腰三角形,![]() 为
为![]() 的中点,
的中点,![]() 为
为![]() 上一点.
上一点.
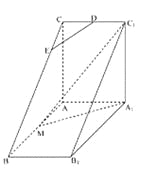
(I)若![]() 平面
平面![]() ,求
,求![]() ;
;
(II)平面![]() 将三棱柱
将三棱柱![]() 分成两个部分,求较小部分与较大部分的体积之比.
分成两个部分,求较小部分与较大部分的体积之比.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校数学课外兴趣小组为研究数学成绩是否与性别有关,先统计本校高三年级每个学生一学期数学成绩平均分(采用百分制),剔除平均分在![]() 分以下的学生后, 共有男生
分以下的学生后, 共有男生![]() 名,女生
名,女生![]() 名,现采用分层抽样的方法,从中抽取了
名,现采用分层抽样的方法,从中抽取了![]() 名学生,按性别分为两组,并将两组学生成绩分为
名学生,按性别分为两组,并将两组学生成绩分为![]() 组, 得到如下频数分布表.
组, 得到如下频数分布表.

(Ⅰ)估计男、女生各自的平均分(同一组数据用该组区间中点值作代表),从计算结果看,能否判断数学成绩与性别有关;
(Ⅱ)规定![]() 分以上为优分(含
分以上为优分(含![]() 分),请你根据已知条件完成
分),请你根据已知条件完成![]() 列联表,并判断是否有
列联表,并判断是否有![]() %以上的把握认为“数学成绩与性别有关”,(
%以上的把握认为“数学成绩与性别有关”,( 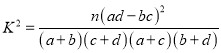 ,其中
,其中![]() )
)

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分)如图,在三棱柱ABC-A1B1C1中,侧棱垂直于底面,AB⊥BC,E、F分别为A1C1和BC的中点.
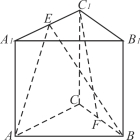
(1)求证:平面ABE⊥平面B1BCC1;
(2)求证:C1F//平面ABE.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆![]() :
: ![]() 的离心率为
的离心率为![]() ,过其右焦点
,过其右焦点![]() 与长轴垂直的直线与椭圆在第一象限相交于点
与长轴垂直的直线与椭圆在第一象限相交于点![]() ,
, ![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设椭圆![]() 的左顶点为
的左顶点为![]() ,右顶点为
,右顶点为![]() ,点
,点![]() 是椭圆上的动点,且点
是椭圆上的动点,且点![]() 与点
与点![]() ,
, ![]() 不重合,直线
不重合,直线![]() 与直线
与直线![]() 相交于点
相交于点![]() ,直线
,直线![]() 与直线
与直线![]() 相交于点
相交于点![]() ,求证:以线段
,求证:以线段![]() 为直径的圆恒过定点.
为直径的圆恒过定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设点![]() 、
、![]() 是平面上左、右两个不同的定点,
是平面上左、右两个不同的定点, ![]() ,动点
,动点![]() 满足:
满足:
![]() .
.
(1)求证:动点![]() 的轨迹
的轨迹![]() 为椭圆;
为椭圆;
(2)抛物线![]() 满足:①顶点在椭圆
满足:①顶点在椭圆![]() 的中心;②焦点与椭圆
的中心;②焦点与椭圆![]() 的右焦点重合.
的右焦点重合.
设抛物线![]() 与椭圆
与椭圆![]() 的一个交点为
的一个交点为![]() .问:是否存在正实数
.问:是否存在正实数![]() ,使得
,使得![]() 的边长为连续自然数.若存在,求出
的边长为连续自然数.若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校夏令营有3名男同学A、B、C和3名女同学X,Y,Z,其年级情况如下表,现从这6名同学中随机选出2人参加知识竞赛(每人被选到的可能性相同).
(1)用表中字母列举出所有可能的结果;
(2)设M为事件“选出的2人来自不同年级且恰有1名男同学和1名女同学”,求事件M发生的概率.
一年级 | 二年级 | 三年级 | |
男同学 | A | B | C |
女同学 | X | Y | Z |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com