
设函数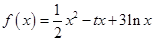 ,
,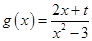 ,已知
,已知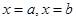 为函数
为函数 的极值点
的极值点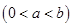
(1)求函数 在
在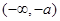 上的单调区间,并说明理由.
上的单调区间,并说明理由.
(2)若曲线 在
在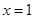 处的切线斜率为-4,且方程
处的切线斜率为-4,且方程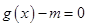 有两个不相等的负实根,求实数
有两个不相等的负实根,求实数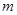 的取值范围.
的取值范围.
(1)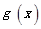 的单调增区间为
的单调增区间为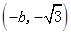 和
和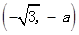 ,
,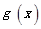 的单调减区间为
的单调减区间为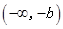
(2)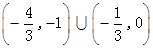 .
.
解析试题分析:(1)
科目:高中数学
来源:
题型:解答题
(本题满分12分)生物体死亡后,它机体内原有的碳14会按确定的规律衰减,大约每经过5730年衰减为原来的一半,这个时间称为“半衰期”.
科目:高中数学
来源:
题型:解答题
(本小题满分12分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区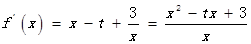 ,
,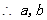 为方程
为方程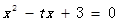 的两根
的两根
又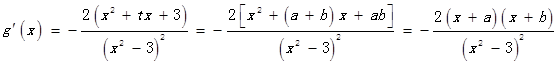
由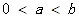 及
及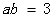 知:
知:
当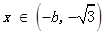 和
和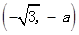 时,
时,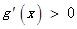 ,当
,当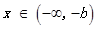 时,
时,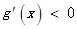
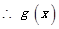 的单调增区间为
的单调增区间为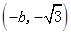 和
和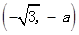 ,
,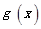 的单调减区间为
的单调减区间为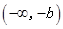
(2)由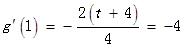 得
得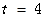
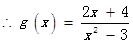
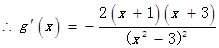
令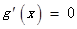 得
得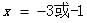
当 在
在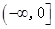 上变化时,
上变化时,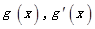 的变化情况如下:
的变化情况如下: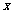
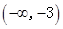
-3 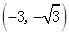
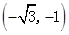
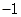 -
-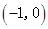
0 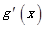
- 0 + + 0 - 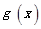
↘ 极小值 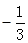
↗

寒假作业大众文艺出版社系列答案
浩鼎文化复习王学期总动员系列答案
君杰文化假期课堂寒假作业系列答案
寒假学习与生活济南出版社系列答案
欢乐寒假福建教育出版社系列答案
智多星寒假生活新疆美术摄影出版社系列答案
寒假天地河北教育出版社系列答案
智乐文化中考备战系列答案
中考妙策33套汇编系列答案
文轩致胜中考系列答案
(Ⅰ)设生物体死亡时体内每克组织中的碳14的含量为1,根据上述规律,写出生物体内碳14的含量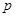 与死亡年数
与死亡年数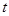 之间的函数关系式;
之间的函数关系式;
(Ⅱ)湖南长沙马王堆汉墓女尸出土时碳14的残余量约占原始含量的76.7℅,试推算马王堆汉墓的年代.(精确到个位;辅助数据: )
)
设函数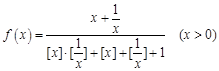 ,其中
,其中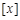 表示不超过
表示不超过 的最大整数,如
的最大整数,如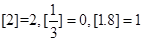 .
.
(1)求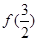 的值;
的值;
(2)若在区间 上存在x,使得
上存在x,使得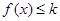 成立,求实数k的取值范围;
成立,求实数k的取值范围;
(3)求函数 的值域.
的值域.
版权声明:本站所有文章,图片来源于网络,著作权及版权归原作者所有,转载无意侵犯版权,如有侵权,请作者速来函告知,我们将尽快处理,联系qq:3310059649。
ICP备案序号: 沪ICP备07509807号-10 鄂公网安备42018502000812号