
(1)求f1(x)=![]() 的不动点;
的不动点;
(Ⅱ)设a>0,且a≠1,求使f2(x)=logax有不动点的a的取值范围.
解:(Ⅰ)x-f1(x)=0,即x-![]() =0,
=0,
解得x1=0,x2=1,x3=-1.
所以,函数f1(x)的不动点为0,1,-1.
(Ⅱ)令g(x)=x-f2(x)-x-logax(x>0),
则g′(x)=1-![]() .
.
(1)若0<a<1,则logae<0, g′(x)>0,
则g(x)在(0,+∞)内单调递增.
又g(a)=a-1<0,g(1)=1>0,所以g(x)=0
即x-f2(x)=0在(0,1)内有一根.
(2)若a>1,则当x∈(0,logae)时,![]() (x)<0,g(x)单调递减,
(x)<0,g(x)单调递减,
当x∈(logae,+∞)时,![]() (x)>0,g(x)单调递增;
(x)>0,g(x)单调递增;
当x=logae时,g(x)有最小值logae-loga(logae).
由g(1)=1>0知,当且仅当logae-loga(logae)≤0时,g(x)=0即x-f2(x)=0有实根.
由a>1,知
logae-loga(logae)≤0![]() logae≤loga(logae)
logae≤loga(logae)![]() e≤logae
e≤logae![]() ae≤e
ae≤e![]() 1<a≤
1<a≤![]() .
.
综合所述,a的取值范围是(0,1)∪![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
| 2 | 2x+1 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| x |
| 1 |
| 2 |
| A、① | B、② | C、①③ | D、①② |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 | 2x+1 |
查看答案和解析>>
科目:高中数学 来源:2013届辽宁省盘锦市高二下期中理科数学试卷(解析版) 题型:选择题
对于函数f(x),在使f(x)≥M成立的所有常数M中,把M中的最大值称为函
数f(x)的“下确界”,则函数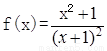 的下确界为( )
的下确界为( )
A. 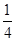 B.
B.
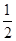 C.
1 D. 2
C.
1 D. 2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com