
【题目】已知关于x的二次函数f(x)=ax2﹣4bx+1. (Ⅰ)设集合A={﹣1,1,2,3,4,5}和B={﹣2,﹣1,1,2,3,4},分别从集合A,B中随机取一个数作为a和b,求函数y=f(x)在区间[1,+∞)上是增函数的概率.
(Ⅱ)设点(a,b)是区域 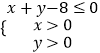 内的随机点,求函数f(x)在区间[1,+∞)上是增函数的概率.
内的随机点,求函数f(x)在区间[1,+∞)上是增函数的概率.
【答案】解:要使函数y=f(x)在区间[1,+∞)上是增函数,则a>0且 ![]() ,即a>0且2b≤a. (Ⅰ)所有(a,b)的取法总数为6×6=36个,满足条件的(a,b)有(1,﹣2),(1,﹣1),(2,﹣2),(2,﹣1),(2,1),(3,﹣2),(3,﹣1),(3,1),(4,﹣2),(4,﹣1),(4,1),(4,2),(5,﹣2),(5,﹣1),(5,1),(5,2)共16个,
,即a>0且2b≤a. (Ⅰ)所有(a,b)的取法总数为6×6=36个,满足条件的(a,b)有(1,﹣2),(1,﹣1),(2,﹣2),(2,﹣1),(2,1),(3,﹣2),(3,﹣1),(3,1),(4,﹣2),(4,﹣1),(4,1),(4,2),(5,﹣2),(5,﹣1),(5,1),(5,2)共16个,
所以,所求概率 ![]() .
.
(Ⅱ)如图,求得区域 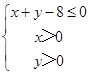 的面积为
的面积为 ![]() .
.
由 ![]() ,求得
,求得 ![]()
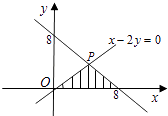
所以区域内满足a>0且2b≤a的面积为 ![]() .
.
所以,所求概率 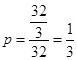
【解析】(Ⅰ)分a=1,2,3,4,5 这五种情况来研究a>0,且 ![]() ≤1的取法共有16种,而所有的取法共有6×6=36 种,从而求得所求事件的概率.(Ⅱ)由条件可得,实验的所有结果构成的区域的面积等于S△OMN=
≤1的取法共有16种,而所有的取法共有6×6=36 种,从而求得所求事件的概率.(Ⅱ)由条件可得,实验的所有结果构成的区域的面积等于S△OMN= ![]() ×8×8=32,满足条件的区域的面积为S△POM=
×8×8=32,满足条件的区域的面积为S△POM= ![]() ×8×
×8× ![]() =
= ![]() ,故所求的事件的概率为 P=
,故所求的事件的概率为 P= ![]() ,运算求得结果.
,运算求得结果.
【考点精析】解答此题的关键在于理解几何概型的相关知识,掌握几何概型的特点:1)试验中所有可能出现的结果(基本事件)有无限多个;2)每个基本事件出现的可能性相等.


 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案科目:高中数学 来源: 题型:
【题目】在某次测量中得到的A样本数据如下:82,84,84,86,86,86,88,88,88,88.若B样本数据恰好是A样本数据都加2后所得数据,则A,B两样本的下列数字特征对应相同的是( )
A.众数
B.平均数
C.中位数
D.标准差
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区植被被破坏,土地沙化越来越严重,最近三年测得沙漠增加值分别为0.2万公顷、0.4万公顷、0.76万公顷,则沙漠增加数y(万公顷)关于年数x的函数关系较为近似的是( )
A.y=0.2x
B.![]()
C.![]()
D.y=0.2+log16x
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),曲线
为参数),曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),在以
为参数),在以![]() 为极点,
为极点, ![]() 轴的正半轴为极轴的极坐标系中,射线
轴的正半轴为极轴的极坐标系中,射线![]() ,与
,与![]() ,
, ![]() 各有一个交点,当
各有一个交点,当![]() 时,这两个交点间的距离为2,当
时,这两个交点间的距离为2,当![]() ,这两个交点重合.
,这两个交点重合.
(1)分别说明![]() ,
, ![]() 是什么曲线,并求出
是什么曲线,并求出![]() 与
与![]() 的值;
的值;
(2)设当![]() 时,
时, ![]() 与
与![]() ,
, ![]() 的交点分别为
的交点分别为![]() ,当
,当![]() ,
, ![]() 与
与![]() ,
, ![]() 的交点分别为
的交点分别为![]() ,求四边形
,求四边形![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]()
(1)判断f(x)的奇偶性并证明;
(2)若f(x)的定义域为[α,β](β>α>0),判断f(x)在定义域上的增减性,并加以证明;
(3)若0<m<1,使f(x)的值域为[logmm(β﹣1),logmm(α﹣1)]的定义域区间[α,β](β>α>0)是否存在?若存在,求出[α,β],若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() (
(![]() )的一个焦点是
)的一个焦点是![]() ,
, ![]() 为坐标原点,且椭圆短轴的两个三等分点与一个焦点构成正三角形,过点
为坐标原点,且椭圆短轴的两个三等分点与一个焦点构成正三角形,过点![]() 的直线交椭圆
的直线交椭圆![]() 于点
于点![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设![]() 为椭圆上一点,且满足
为椭圆上一点,且满足![]() ,当
,当![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若a,b是函数f(x)=x2﹣px+q(p>0,q>0)的两个不同的零点,c<0且a,b,c这三个数可适当排序后成等差数列,也可适当排序后成等比数列,则 ![]() ﹣2c的最小值等于( )
﹣2c的最小值等于( )
A.9
B.10
C.3
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=(x﹣1)ex﹣kx2(k∈R).
(1)当k=1时,求函数f(x)的单调区间;
(2)当 ![]() 时,求函数f(x)在[0,k]上的最大值M.
时,求函数f(x)在[0,k]上的最大值M.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an} 中,a1=1,a2= ![]() ,且
,且 ![]() (n=2,3,4,…)
(n=2,3,4,…)
(1)求a3、a4的值;
(2)设bn= ![]() (n∈N*),试用bn表示bn+1并求{bn} 的通项公式;
(n∈N*),试用bn表示bn+1并求{bn} 的通项公式;
(3)设cn= ![]() (n∈N*),求数列{cn}的前n项和Sn .
(n∈N*),求数列{cn}的前n项和Sn .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com