
【题目】已知数列{an} 中,a1=1,a2= ![]() ,且
,且 ![]() (n=2,3,4,…)
(n=2,3,4,…)
(1)求a3、a4的值;
(2)设bn= ![]() (n∈N*),试用bn表示bn+1并求{bn} 的通项公式;
(n∈N*),试用bn表示bn+1并求{bn} 的通项公式;
(3)设cn= ![]() (n∈N*),求数列{cn}的前n项和Sn .
(n∈N*),求数列{cn}的前n项和Sn .
【答案】
(1)解:∵数列{an} 中,a1=1,a2= ![]() ,
,
且 ![]() (n=2,3,4,),
(n=2,3,4,),
∴ ![]() =
= ![]() =
= ![]() ,
,
![]() =
= ![]() =
= ![]() ,
,
∴ ![]() ,
, ![]() .
.
(2)解:当n≥2时, ![]() ,
,
∴当n≥2时, ![]() ,
,
故 ![]() ,
,
累乘得bn=nb1,
∵b1=3,∴bn=3n,n∈N*.
(3)解:∵ ![]()
= ![]() ,
,
∴Sn=c1+c2+…+cn
=(tan6﹣tan3)+(tan9﹣tan6)+…+(tan(3n+3)﹣tan3n)
=tan(3n+3)﹣tan3.
【解析】(1)由数列{an} 中,a1=1,a2= ![]() ,且
,且 ![]() (n=2,3,4,…),分别令n=2和n=3,能求出a3、a4的值.(2)当n≥2时,
(n=2,3,4,…),分别令n=2和n=3,能求出a3、a4的值.(2)当n≥2时, ![]() ,故当n≥2时,
,故当n≥2时, ![]() ,所以
,所以 ![]() ,由累乘法能用bn表示bn+1并求出{bn} 的通项公式.(3)由
,由累乘法能用bn表示bn+1并求出{bn} 的通项公式.(3)由 ![]() =tan(3n+3)﹣tan3n,能求出数列{cn}的前n项和Sn .
=tan(3n+3)﹣tan3n,能求出数列{cn}的前n项和Sn .
【考点精析】关于本题考查的数列的前n项和和数列的通项公式,需要了解数列{an}的前n项和sn与通项an的关系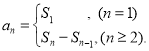 ;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式才能得出正确答案.
;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式才能得出正确答案.


 一线名师提优试卷系列答案
一线名师提优试卷系列答案科目:高中数学 来源: 题型:
【题目】已知关于x的二次函数f(x)=ax2﹣4bx+1. (Ⅰ)设集合A={﹣1,1,2,3,4,5}和B={﹣2,﹣1,1,2,3,4},分别从集合A,B中随机取一个数作为a和b,求函数y=f(x)在区间[1,+∞)上是增函数的概率.
(Ⅱ)设点(a,b)是区域 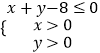 内的随机点,求函数f(x)在区间[1,+∞)上是增函数的概率.
内的随机点,求函数f(x)在区间[1,+∞)上是增函数的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知正三棱柱ABC=A1B1C1的各棱长都是4,E是BC的中点,动点F在侧棱CC1上,且不与点C重合.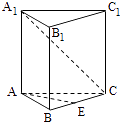
(1)当CF=1时,求证:EF⊥A1C;
(2)设二面角C﹣AF﹣E的大小为θ,求tanθ的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为贯彻“激情工作,快乐数学”的理念,某学校在学习之余举行趣味知识有奖竞赛,比赛分初赛和决赛两部分,为了增加节目的趣味性,初赛采用选手选一题答一题的方式进行,每位选手最多有5次选答题的机会,选手累计答对3题或答错3题即终止其初赛的比赛,答对3题者直接进入决赛,答错3题者则被淘汰,已知选手甲答题的正确率为 ![]() .
.
(1)求选手甲答题次数不超过4次可进入决赛的概率;
(2)设选手甲在初赛中答题的个数ξ,试写出ξ的分布列,并求ξ的数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 过点
过点![]() ,其离心率为
,其离心率为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)直线![]() 与
与![]() 相交于
相交于![]() 两点,在
两点,在![]() 轴上是否存在点
轴上是否存在点![]() ,使
,使![]() 为正三角形,若存在,求直线
为正三角形,若存在,求直线![]() 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在实数集R中定义一种运算“⊙”,具有性质:①对任意a、b∈R,a⊙b=b⊙a;②a⊙0=a;③对任意a、b∈R,(a⊙b)⊙c=(ab)⊙c+(a⊙c)+(b⊙c)﹣2c,则函数f(x)=x⊙ ![]() 的最小值是( )
的最小值是( )
A.2
B.3
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2cosxsin(x+ ![]() )﹣
)﹣ ![]() sin2x+sinxcosx.
sin2x+sinxcosx. 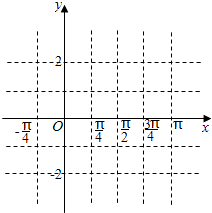
(1)当x∈[0, ![]() ]时,求f(x)的值域;
]时,求f(x)的值域;
(2)用五点法在图中作出y=f(x)在闭区间[﹣ ![]() ,
, ![]() ]上的简图;
]上的简图;
(3)说明f(x)的图象可由y=sinx的图象经过怎样的变化得到?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com