
【题目】已知数列![]() 满足对任意的
满足对任意的![]() 都有
都有![]() ,且
,且![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)设数列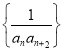 的前
的前![]() 项和为
项和为![]() ,不等式
,不等式![]() 对任意的正整数
对任意的正整数![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() (2)
(2)![]()
【解析】试题分析:
(1)当n=1,n=2时,直接代入条件![]() 且
且![]() ,可求得;
,可求得;
(2)递推一项,然后做差得![]() ,所以
,所以![]() ;由于
;由于![]() ,即当
,即当![]() 时都有
时都有![]() ,所以数列
,所以数列![]() 是首项为1,公差为1的等差数列,故求得数列
是首项为1,公差为1的等差数列,故求得数列![]() 的通项公式;
的通项公式;
(3)由(2)知![]() ,则
,则![]() ,利用裂项相消法得
,利用裂项相消法得![]() ,根据
,根据![]() 单调递增得
单调递增得![]() ,要使不等式
,要使不等式![]() 对任意正整数n恒成立,只要
对任意正整数n恒成立,只要![]() ,即可求得实数a的取值范围.
,即可求得实数a的取值范围.
试题解析:
(1)解:当![]() 时,有
时,有![]() ,
,
由于![]() ,所以
,所以![]() .
.
当![]() 时,有
时,有![]() ,
,
将![]() 代入上式,由于
代入上式,由于![]() ,所以
,所以![]() .
.
(2)解:由于![]() ,①
,①
则有![]() .②
.②
②-①,得![]() ,
,
由于![]() ,所以
,所以![]() ③
③
同样有![]() ,④
,④
③-④,得![]() .
.
所以![]() .
.
由于![]() ,即当
,即当![]() 时都有
时都有![]() ,
,
所以数列![]() 是首项为1,公差为1的等差数列.
是首项为1,公差为1的等差数列.
故![]() .
.
(3)解:由(2)知![]() ,则
,则![]() ,所以
,所以
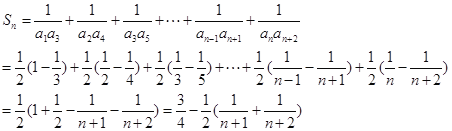
![]() ,∴数列
,∴数列![]() 单调递增 .
单调递增 .
![]() .
.
要使不等式![]() 对任意正整数n恒成立,只要
对任意正整数n恒成立,只要![]() .
.
![]() .
.
![]() ,即
,即![]() .
.
所以,实数a的取值范围是![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知函数 ![]()
(1)判断f(x)的奇偶性并证明;
(2)若f(x)的定义域为[α,β](β>α>0),判断f(x)在定义域上的增减性,并加以证明;
(3)若0<m<1,使f(x)的值域为[logmm(β﹣1),logmm(α﹣1)]的定义域区间[α,β](β>α>0)是否存在?若存在,求出[α,β],若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某公司的职工食堂中,食堂每天以3元/个的价格从面包店购进面包,然后以5元/个的价格出售.如果当天卖不完,剩下的面包以1元/个的价格卖给饲料加工厂.根据以往统计资料,得到食堂每天面包需求量的频率分布直方图如图所示.食堂某天购进了 90个面包,以![]() (个)(其中
(个)(其中![]() )表示面包的需求量,
)表示面包的需求量, ![]() (元)表示利润.
(元)表示利润.
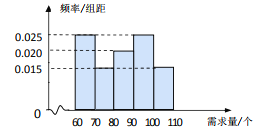
(1)根据直方图计算需求量的中位数;
(2)估计利润![]() 不少于100元的概率;
不少于100元的概率;
(3)在直方图的需求量分组中,以需求量落入该区间的频率作为需求量在该区间的概率,求![]() 的数学期望.
的数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() =1(a>b>0)与y轴的交点为A,B(点A位于点B的上方),F为左焦点,原点O到直线FA的距离为
=1(a>b>0)与y轴的交点为A,B(点A位于点B的上方),F为左焦点,原点O到直线FA的距离为 ![]() b.
b.
(1)求椭圆C的离心率;
(2)设b=2,直线y=kx+4与椭圆C交于不同的两点M,N,求证:直线BM与直线AN的交点G在定直线上.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an} 中,a1=1,a2= ![]() ,且
,且 ![]() (n=2,3,4,…)
(n=2,3,4,…)
(1)求a3、a4的值;
(2)设bn= ![]() (n∈N*),试用bn表示bn+1并求{bn} 的通项公式;
(n∈N*),试用bn表示bn+1并求{bn} 的通项公式;
(3)设cn= ![]() (n∈N*),求数列{cn}的前n项和Sn .
(n∈N*),求数列{cn}的前n项和Sn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某联欢晚会举行抽奖活动,举办方设置了甲、乙两种抽奖方案,方案甲的中奖率为 ![]() ,中奖可以获得2分;方案乙的中奖率为P0(0<P0<1),中奖可以获得3分;未中奖则不得分.每人有且只有一次抽奖机会,每次抽奖中奖与否互不影响,晚会结束后凭分数兑换奖品. (Ⅰ)张三选择方案甲抽奖,李四选择方案乙抽奖,记他们的累计得分为X,若X≤3的概率为
,中奖可以获得2分;方案乙的中奖率为P0(0<P0<1),中奖可以获得3分;未中奖则不得分.每人有且只有一次抽奖机会,每次抽奖中奖与否互不影响,晚会结束后凭分数兑换奖品. (Ⅰ)张三选择方案甲抽奖,李四选择方案乙抽奖,记他们的累计得分为X,若X≤3的概率为 ![]() ,求P0;
,求P0;
(Ⅱ)若张三、李四两人都选择方案甲或都选择方案乙进行抽奖,问:他们选择何种方案抽奖,累计得分的数学期望较大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() 的部分图象如图所示,则下列结论错误的是( )
的部分图象如图所示,则下列结论错误的是( ) 
A.![]()
B.函数f(x)在 ![]() 上单调递增
上单调递增
C.函数f(x)的一条对称轴是 ![]()
D.为了得到函数f(x)的图象,只需将函数y=2cosx的图象向右平移 ![]() 个单位
个单位
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将函数y=sin(x﹣ ![]() )的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再将所得图象向左平移
)的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再将所得图象向左平移 ![]() 个单位,则所得函数图象对应的解析式为( )
个单位,则所得函数图象对应的解析式为( )
A.y=sin( ![]() x﹣
x﹣ ![]() )
)
B.y=sin(2x﹣ ![]() )
)
C.y=sin ![]() x
x
D.y=sin( ![]() x﹣
x﹣ ![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com