
| A. | 由(1+1)2>21,(2+1)2>22,(3+1)2>23,…,推断:对一切n∈N*,(n+1)2>2n | |
| B. | 由f(x)=xcosx满足f(-x)=-f(x)对?x∈R都成立,推断:f(x)=xcosx为奇函数 | |
| C. | 由圆x2+y2=r2的面积S=πr2,推断:椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1的面积S=πab | |
| D. | 由an=2n-1,求出S1=12,S2=22,S3=32,…,推断:数列{an}的前n项和Sn=n2 |
分析 对于A,举出反例:(6+1)2=49<26=64,可判断A错误;
对于B,是奇函数的定义,不是归纳推理,可判断B错误;
对于C,是类比推理,可判断C错误;
对于D,由个别到一般,是归纳推理且结论正确,可判断D正确.
解答 解:对于A,由(1+1)2>21,(2+1)2>22,(3+1)2>23,…,推断:对一切n∈N*,(n+1)2>2n,错误,如(6+1)2=49<26=64,故A错误;
对于B,由f(x)=xcosx满足f(-x)=-f(x)对?x∈R都成立,推断:f(x)=xcosx为奇函数,是奇函数的定义,不是归纳推理,故B错误;
对于C,由圆x2+y2=r2的面积S=πr2,推断:椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1的面积S=πab是类比推理.故C错误;
对于D,由an=2n-1,求出S1=12,S2=22,S3=32,…,推断:数列{an}的前n项和Sn=n2,是归纳推理且结论正确,故D正确.
故选:D.
点评 本题考查命题的真假判断与应用,区分合情推理中的归纳推理与类比推理的区别是正确判断的关键,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | {x|-2<x<1} | B. | {x|-1<x<2} | C. | {x|x<-2或x>1} | D. | {x|x<-1或x>2} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (3,-1) | B. | (-3,1) | C. | (-3,-1) | D. | (3,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | 2023×2017 | B. | 2023×2016 | C. | 1008×2023 | D. | 2017×1008 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
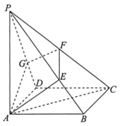 如图,在四棱锥P-ABCD中,底面ABCD为正方形,PA丄底面ABCD,PA=AC.过点A的平面与棱PB,PC,PD分别交于点E,F,G(E,F,G三点均不在棱的端点处).
如图,在四棱锥P-ABCD中,底面ABCD为正方形,PA丄底面ABCD,PA=AC.过点A的平面与棱PB,PC,PD分别交于点E,F,G(E,F,G三点均不在棱的端点处).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com